Nous avons déjà vu, dans le cadre général de l'approche monofocale des conique que le passage à la limite dans le théorème de Poncelet donne, par continuité, l'existence de la tangente en tout point d'une conique.

Comme nous n'avons pas encore abordé ce théorème dans les premières pages sur la parabole, nous proposons une approche spécifique à cette courbe. Par rapport aux programmes actuels qui traitent de la tangente à une conique, en général par étude de courbe aprés l'équation réduite, nous favorisons dans ce site de géométrie une argumentation géométrique, et donc, à nouveau la tangente comme limite de sécantes.

Existence de la tangente en un point d'une parabole

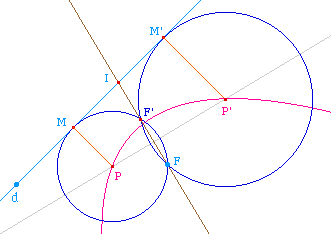
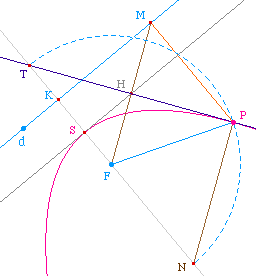
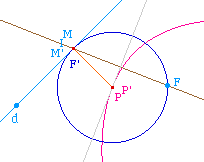
Lorsque l'on fait déplacer P' et le rapprocher de P, M' se rapproche de M et I aussi. Dans l'égalité IM2 = IF.IF', IF est non nul car le foyer n'appartient pas à directrice. Donc si IM tend vers 0 cela signifie que IF' aussi et donc que F' tend vers I, c'est-à-dire M. Autrement dit, la droite (PP'), médiatrice de [FF'], admet une position limite quand P' tend vers P qui est la médiatrice de [FM]. Comme le triangle FPM est isocèle par construction, cette médiatrice est aussi bissectrice intérieure de l'angle FPM. 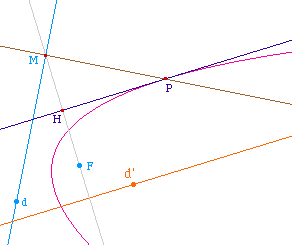La figure PBTgt1.fig ci-contre pour illustration.

En tout point P d'une parabole existe une tangente qui est la médiatrice de [FM] où M est la projection orthogonale de P sur la directrice.

Autrement dit, dans la construction "par point", où P est construit à partir de M sur la directrice par intersection de la perpendiculaire en M à la directrice et la médiatrice de [FM], on construit à la fois un point de la parabole mais en même temps la tangente en ce point.

Cela signifie aussi qu'une droite est tangente à la parabole de foyer F et de directrice d si et seulement si le symétrique de F par rapport à cette droite appartient à la directrice.

	En particulier, si on note Q l'intersection de la tangente en P avec la directrice, le triangle PFQ étant le symétrique par rapport à la tangente du triangle PMQ, l'angle de PFQ en F est droit. Ce resultat est par ailleurs une propriété générale des coniques.
	Remarques : la tangente au sommet de la parabole est parallèle à la directrice. Elle est l'image de la directrice dans l'homothétie de centre F de rapport 1/2. L'image de la projection M dans cette homothétie est donc sur cette tangente au sommet

Sous-tangente et sous-normale

La tangente en P à la parabole coupe sont axe en T et sa normale le coupe en N. Soit U la projection orthogonale de P sur l'axe. On appelle : Sous tangente le segment [TU] et Sous-normale le segment [UN]. On sait que, H est milieu de [FM], et que (MP) est parallèle à l'axe (FT). Donc la symétrie centrale de centre H envoie M en F et P sur l'intersection de la tangente avec l'axe, soit en T. Donc le quadrilatère MTFP est un prallèlogramme. Comme de plus ses diagonales sont orthogonales, c'est un losange. H étant milieu de [PT], par projection S est milieu de [TU] : Le sommet de la parabole est milieu de toute sous-tangente.

Par ailleurs le quadrilatère MFNP est aussi un parallélogramme car il a ses côtés opposés deux à deux parallèles ([MF] :: [NP] car les deux sont perpendiculaires à la tangente). D'où les égalités : FN = MP = TF = FP. Ainsi le cercle de centre F passant par P coupe l'axe en T et N ce qui donne une autre construction élémentaire de la tangente à une parabole en un point. Enfin, puisque TF = FN et que (illustration précédente) les triangles TKN et FUP ont les trois côtés deux à deux parallèles dont deux de même longueurs, ils sont isométriques, en particulier TK = FU, soit encore KS = UN, d'où : Pour tout point P d'une parabole, sa sous tangente a pour longueur la valeur du paramètre de la parabole. La figure PBTgt2.fig ci-contre.

Une première application

On considère une parabole de foyer F et de directrice d'.On s'intéresse à la construction des tangentes à cette parabole parallèles à une droite donnée d'.

Une telle tangente cherchée sera médiatrice de [FM] où est est la projection sur la directrice du point de contact P de la tangente et de la parabole. Ce point M est trés facilement accessible, c'est tout simplement l'intersection de d avec la perpendiculaire à d' en F. Celle-ci existe si d' n'est pas parallèle à l'axe de la parabole. Et alorsl n'y a qu'un point M possible : Pour toute droite du plan non parallèle à l'axe d'une parabole, il existe une et une seule tangente à la parabole parallèle à cette droite. La figure PBTgt3.fig ci-contre. La macro TPParall.mac d'objets initiaux F, d et la droite d'. La macro renvoie la tangente et le point de contact.

Tangentes et droite de Steiner

Réciproquement

Soient ABC un triangle et F un point de son cercle circonscrit, autre que les points A, B, et C. Alors la parabole de foyer F et de directrice la droite de Steiner de F relative au triangle est nécessairement tritangente aux côtés du triangle.

La figure PBTgt5.fig correspondante.

Les macros "tangente en un point" d'une parabole

Les constructions précédentes aboutissent à une première macro-construction

Charger la macro TgtParaF.mac d'objets initiaux F, d et un point P de la parabole de foyer F et de directrice d.

On peut aussi utiliser une macro qui n'a comme abjets initiaux que la parabole et un point lui appartenant. Cette macro a été construite à partir de la notion de rayon conjugué dans cette page de présentation projective sur les coniques par Michel Guillerault.

Charger la macro TgtePara.mac d'objets initiaux un point P de la parabole et la parabole.

Remarques : Sur la figure Cabri PBDrt3.fig illustrant la notion de diamètre conjugué vu à la page précédente, on remarquera que la droite d'₀ est la tangente à la parabole en J₀. En fait, la tangente est la direction conjuguée au diamètre passant par le point dont on cherche la tangente. Ces points seront abordés ultérieurement dans des pages de compléments sur les formes quadratiques et les coniques.

Menu général