Preuve du résultat sur l'orthocentre

Les Définitions

 

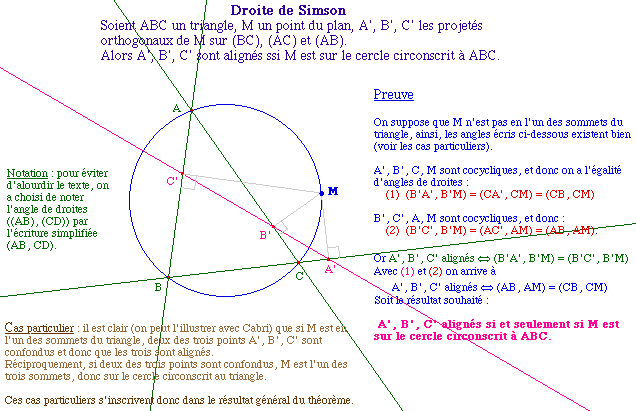
  Simson1.fig

 

 

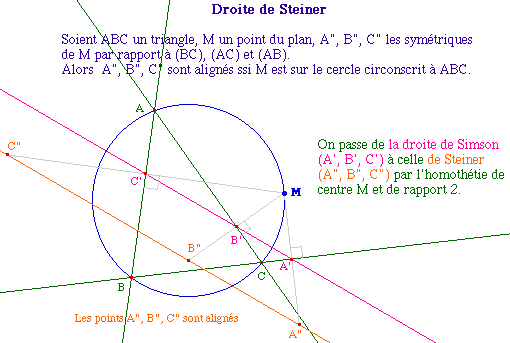
Steiner1.fig

 

Une première propriété

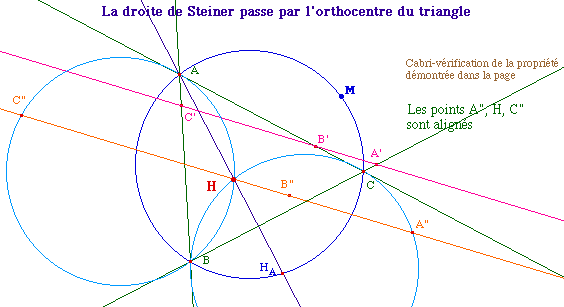
Steiner2.fig

Preuve de ce résultat

H désigne l'orthocentre du triangle ABC, A", B", C" les symétriques de M par rapport à (BC), (CA) et (CB). M est sur le cercle circonscrit à ABCdonc ces trois points sont alignés.

On a vu à la page sur l'orthocentre que le symétrique du cercle circonscrit par rapport aux côtés du triangle passe par l'orthocentre. Ainsi - ci dessus sur les deux cercles en bleu clair symétriques du cercle circonscrit par rapport à (BC) et (AB) - on a que B, H, C et A" sont cocycliques car c'est le cas de B, H_A, C et M. Pour la même raison C", A, H, B sont coycliques.

 

- B, H, C et A" sont cocycliques donc, en angles de droites, (HA", HB) = (CA", CB).

- C", A, H, B sont coycliques, de même, (HB, HC") = (AB, AC").

On peut alors écrire (HA", HC") = (HA", HB) + (HB, HC") = (CA", CB) + (AB, AC").

Mais, les symétries orthogonales changeant les angles en leurs opposés, on a (CA", CB) = - (CM, CB) et (AB, AC") = - (AB, AM).

Il en résulte donc que (HA", HC") = (CB, CM) + (AM, AB) = 0 car A, B, C et M sont cocycliques.

Ainsi donc H est sur la droite (A"C"), c'est-à-dire sur la droite de Steiner.

Haut

Application : une deuxième propriété

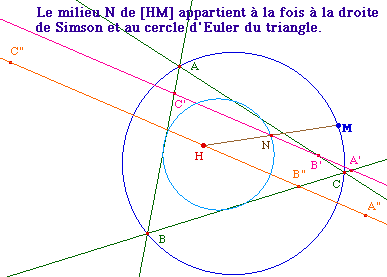
En effet, l'homothétie de centre M de rapport 1/2 transforme la droite de Steiner en la droite de Simpson et donc le milieu de [HM] appartient à cette dernière. De plus, l'homothétie de centre H et de rapport 1/2 transforme le cercle circonscrit à un triangle en son cercle d'Euler et donc le milieu de [HM] appartient aussi au cercle d'Euler.   Steiner3.fig

Haut

Menu général