Droites de Simson et Steiner
5 - Autres propriétés de ces droites

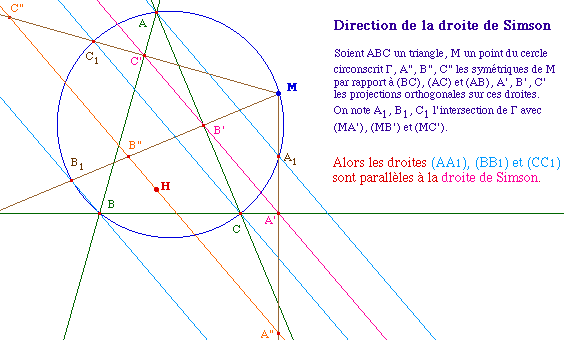
[1 - Existence et premières propriétés] [2 - Parabole tritangente à un triangle]
[3 - Point de Miquel d'un quadrilatère complet et Parabole] [4 - Enveloppe des droites de Simson]

[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]

  

 

Direction de la droite de Simson

 

  
  DirSim1.fig

La preuve est immédiate :

(A1M, A1A) = (CM, CA) = (CM, CB') = (A'M, A'B') et donc les droites (AA1) et (A'B') sont parallèles.

 

Angle entre deux droites de Simson S(M) et S(M')

 

 

AnglSim1.fig

 

Généralisation à un angle quelconque

 

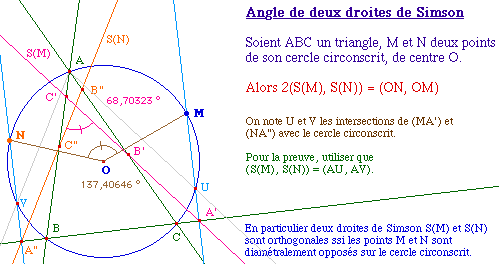
On doit à Poncelet l'idée de généraliser la projection orthogonale de droite de Simson à un angle quelconque : on a toujours une droite, cela se montre par cocyclicité comme dans le cas particulier où la cocyclicité est issue de deux angles droits

 

GeneSim.fig

 

[1 - Existence et premières propriétés] [2 - Parabole tritangente à un triangle]
[3 - Point de Miquel d'un quadrilatère complet et Parabole] [4 - Enveloppe des droites de Simson]

[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]

 

Menu général