|
|
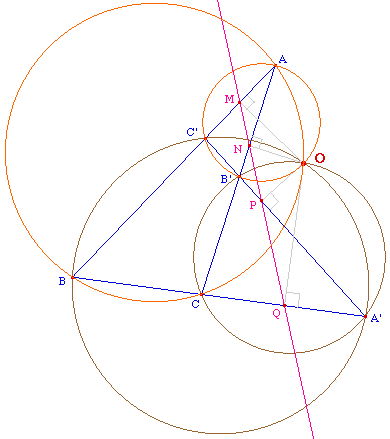
ABC un triangle et la transversale (A'B'C') forment un quadrilatère complet.Soit O l'autre intersection des cercles circonscrits à ABC et AB'C'. La droite de Simson de O par rapport à ABC est la droite passant par M, N, et Q. Celle de O relative à AB'C' est la droite passant par M, N et P.Donc les points M, N, P et Q sont alignés.L'alignement de N, P et Q entraine de O est sur le cercle circonscrit à B'CA'.L'alignement de M, P, et Q entraine que O est sur le cercle corconscrit à BA'C'.
Ainsi, les cercles circonscrits aux 4 triangles sont concourants en un point appelé point de Miquel du quadrilatère complet.Conséquence : la droite de Steiner de O par rapport aux quatre triangles contient les 4 orthocentres des triangles qui sont donc alignés.Autre preuve par le théorème du Pivot Une autre preuve classique : elle est basée sur le fait que O est le centre de la similitude directe qui envoie C en B' et B en C'. |