La droite de Simson :

Les projections orthogonales d'un point sur les trois côtés d'un triangle sont alignés si et seulement si ce point appartient au cercle circonscrit au triangle. Dans ce cas, la droite passant par ces trois points s'appelle la droite de Simson.

 

L'enveloppe et première propriété

 

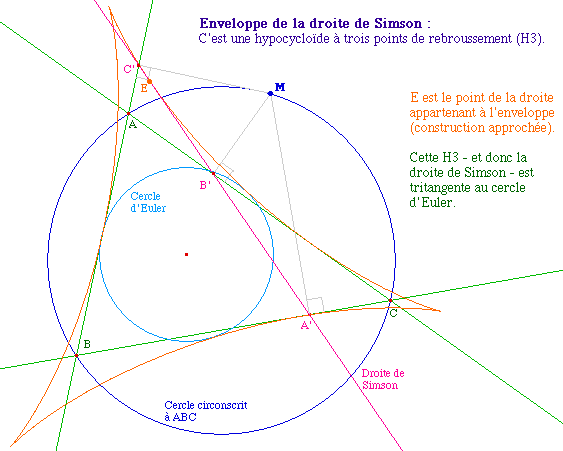
  EnvSim1.fig

Eléments de preuve

Pour montrer ce résultat, il faut une caractérisation géométrique des hypocycloïde à 3 points de rebroussement (H3 dans la suite) que l'on retrouvera sur la figure ci-dessous (preuve par équation paramétrique).

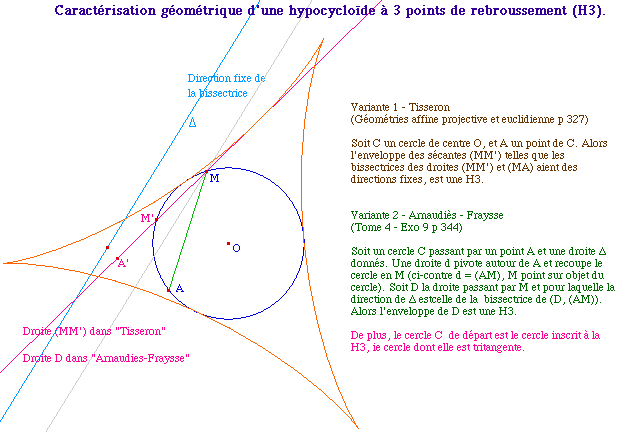
PropH3G.fig

 

Utilisation de cette caractérisation (version Arnaudiès)

 

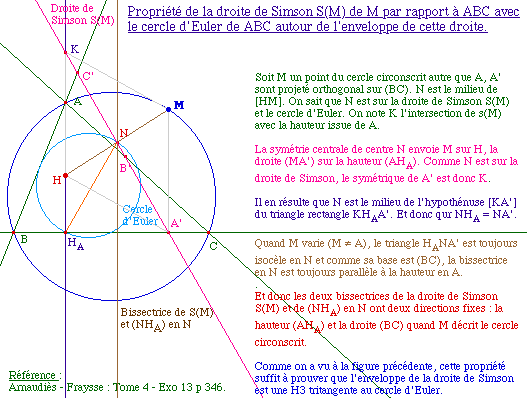
  EnvSim2.fig

 

Autre construction et propriété relative à l'enveloppe de la droite de Simson

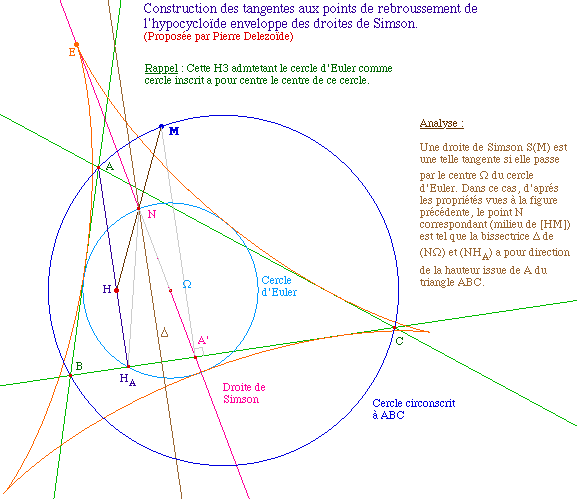
  EnvSim3.fig

Or on dispose du résultat suivant, que le lecteur est invité à redémontrer
Voir par exemple CAPES externe 97 - seconde épreuve - Partie I pour des détails plus précis sur ce point.

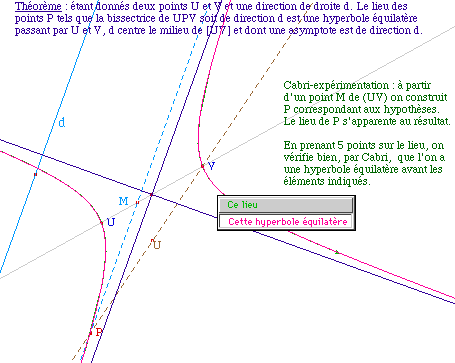
HypEqui1.fig

L'hyperbole équilatère se construit facilement. Cela permet de construire les points N qui donnent les tangentes aux points de rebroussement.

 

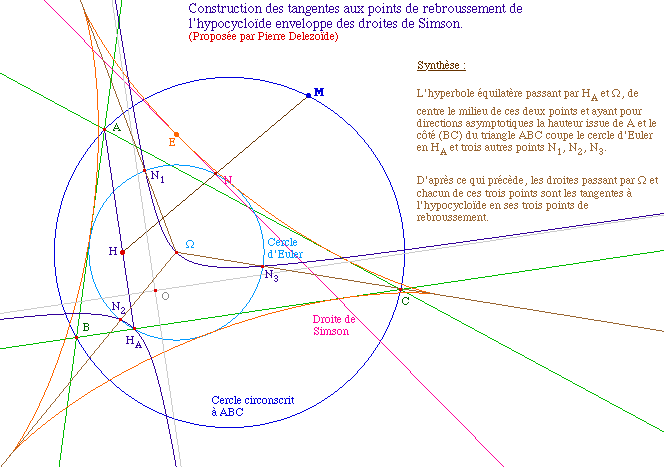
EnvSim4.fig

Un résultat général sur les hyperboles équilatère fait que le triangle N₁N₂N₃ est équilatéral. En effet, on sait que :

Soient A et B deux points d'une hyperbole équilatère. Alors le cercle de centre A passant par B recoupe l'hyperbole en trois points qui forment un triangle équilatéral.

 

Direction de l'hypocycloïde

Dans une H3, on sait que le rayon du cercle circonscrit est trois fois celui du cercle inscrit. Cette propriété permet de construire les points de rebroussement de l'hypocycloïde, ce sont les homothétiques de N₁, N₂, N₃ dans l'homothétie centrée au centre du cercle d'Euler et de rapport 3. Autrement dit, dans la construction précédente le triangle N₁N₂N₃ donne l'orientation de l'hypocycloïde.

On notera également que le symétrique N'₁N'₂N'₃ de N₁N₂N₃ par raport au centre du cercle d'Euler donnent les points de contact du cercle d'Euler avec l'hypocycloïde.

Un autre résultat remarquable est que cette direction est celle du triangle de Morley obtenu à partir des trissectrices de ABC (le triangle PQR ci-dessous). On a donc deux constructions dans un triangle quelconque qui aboutissent à une symétrie d'ordre 3, et de plus, avec la même orientation.

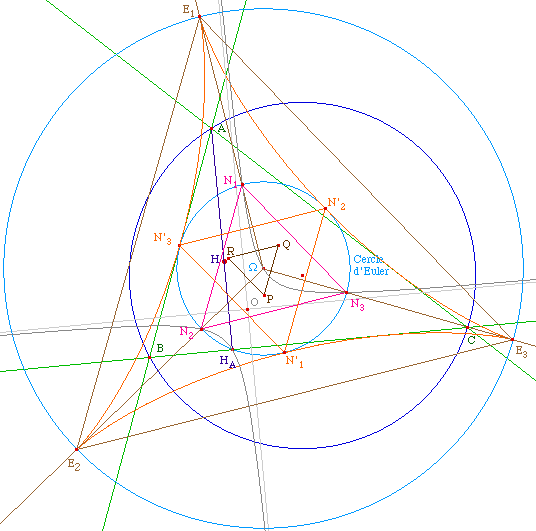
EnvSim5.fig

Menu général