|
|
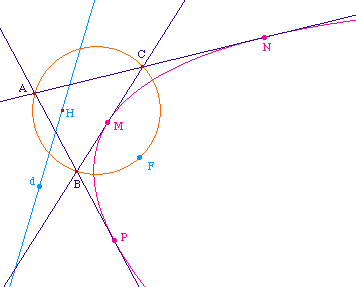
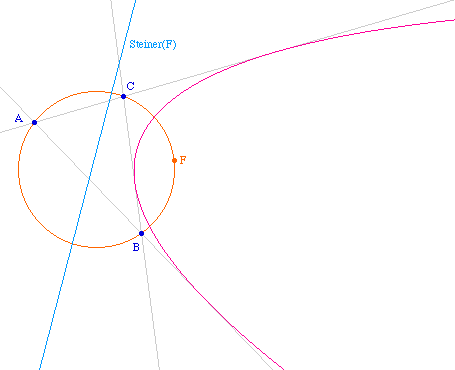
Soient alors trois tangentes issues de trois points M, N et P d'une parabole de foyer F et de directrice d. On sait que les symétriques de F par rapport à chaque tangente appartient à la directrice. Ils sont donc alignés, et ainsi F appartient au cercle circonscrit au triangle ABC formé des intersections des tangentes prises 2 à 2, et la directrice est la droite de Steiner pour le triangle ABC associé au foyer de la parabole. La directrice passe donc par l'orthocentre du triangle.
|