La parabole, comme conique d'excentricité unique, nécessite des développements spécifiques.Toutefois rappelons que de nombreuses propriétés générales sur les coniques, dans leur approche monofocale, restent valides (le théorème de Poncelet par exemple).

Définitions

Définition 1 : soient d une droite et F un point n'appartenant pas à d, on appelle parabole de foyer F et de directrice d l'ensemble des points équidistants de F et d. MF = MH C'est aussi clairement l'ensemble des centres des cercles passant par F et tangents à d. Définition 2 : une courbe P du plan est dite une parabole s'il existe un couple (d, F) tel que P soit l'ensemble des points équidistants de F et d. La seconde définition nécessite de montrer l'unicité du couple (d, F), ce qui sera fait avoir observé quelques premières propriétés de la définition 1.

Axe et sommet

Soit K la projection orthogonale de F sur la directrice. Par définition même de la parabole, celle-ci admet l'axe (FK) comme axe de symétrie, appelé axe focal de la parabole, ou plus simplement axe de la parabole. Sur l'axe focal, il n'y a qu'un point de la parabole, le milieu S de [FK]. S est l'intersection de l'axe focal et de la médiatrice de [FK]. Il est alors immédiat que les points à égale distance de F et de d sont du même côté que F de la médiatrice de [FK], ce qui signifie que la parabole est d'un même côté de cette droite. C'est la raison pour laquelle S est aussi appelé sommet de la parabole.   PBIntro1.fig ci-contre.

Construction de la parabole

Construction "par point"   Quand un point H décrit la directrice d, la médiatrice de [FH] coupe la perpendiculaire à d en H en un point de la parabole de foyer F et de directrice d. Ce point est le seul de la parabole appartenant à la perpendiculaire à la directrice issue de H. Par ailleurs il est dans le même demi-plan que F, c'est une autre façon de conclure que la parabole est dans le demi-plan contenant F délimité par la directrice. Cette construction montre aussi que la parabole admet deux branches infinies.

Construction à l'équerre   Une corde de longueur OA a une extrémité fixée en F et l'autre en M sur une équerre dont le côté [HM] de l'angle droit a même longueur OA que la corde. Alors quand H décrit une partie de la directrice de la parabole, le point P de la corde tendue décrit une portion de parabole. En effet, si la corde est tendue, le point P prend une position telle que MP + PF = HM. Autrement dit PF = PH donc P est bien sur la parabole de foyer F et de directrice P PBIntro2.fig ci-contre. Remarque (cosmétique) : La figure proposée a été construite pour que le point P prenne toutes les positions possibles de l'équerre quand H décrit un segment de la droite. C'est la raison pour laquelle on observera que les extrémités du lieu sont ici fermées par Cabri, alors qu'elles seraient ouvertes si H parcourrait la droite.

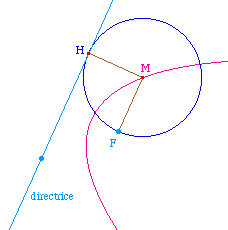
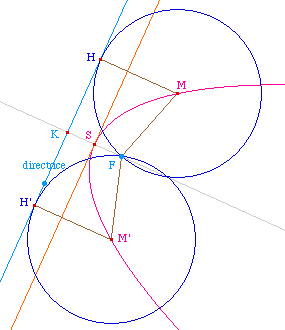
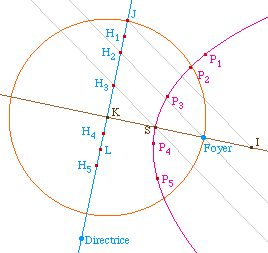
Réalisation d'une macro À partir du foyer et de sa projection K, on construit le sommet S et I d'abscisse 3 dans le repère (K, S). Ceci permet de construire H2 et H3 d'abscisse 2/3 et 1/3 dans le repère (K, J) de la directrice (KJ = KF le paramètre de la parabole). Dans ce repère (K, S), les autres points ont pour abscisse H1 (5/6), H4 (-1/6) et H5 (-1/2). On n'utilise donc pas le sommet ni aucun couple de points symétriques par rapport à l'axe dans la construction de la parabole par les cinq points P1, P2, P3, P4, P5. Cela permet à cette macro de produire une parabole sur laquelle les macros "réciproques" sont toutes applicables.   La macro ParaFD.mac qui construit une parabole à partir de sa directrice et de son foyer.

Intérieur de la parabole

Définition générale

Si une conique définie par foyer, directrice et excentricité est donnée par la relation MF/MH = e, on appelle intérieur de la conique l'ensemble des points du plan pour lesquels MF/MH < e et extérieur ceux pour lesquels MF/MH > e.

Cas de la parabole

Dans la construction par point ci-dessus, il est clair qu'un point M1 appartenant à la demi-droite [MH) est plus prés de H que de F (de par la médiatrice de [FH], et qu'il est donc à l'extérieur de la parabole. De même, un point M2 sur l'autre demi-droite de (MH) est plus prés de F que de H donc à l'intérieur de la parabole. L'intérieur de la parabole est la partie du plan qu'elle délimite contenant le foyer.

Menu général