|
|
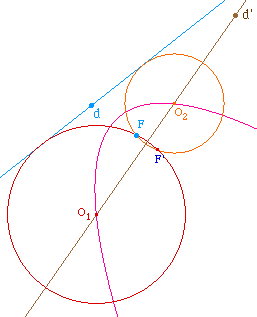
Or I reste fixe tant que la direction (FF') est fixe,
c'est-à-dire tant que la droite d' se déplace
parallélement à elle-même : dans ce cas
I est milieu des points de contact des cercles et donc
projection du milieu des intersections de la parabole avec
une droite de direction donnée.
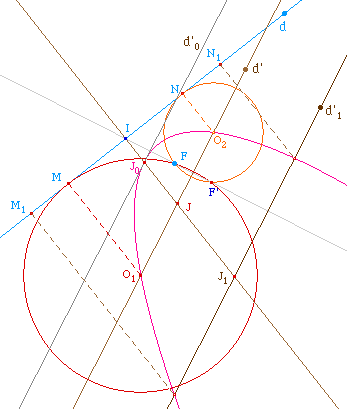
Sur l'illustration ci-dessus, quand d'1 se
déplace, parallèlement à d', le lieu du
milieu J1 des points d'intersection de
d'1 avec la parabole est une demi-droite
[J0J). J0 se construit à
partir de d'0 médiatrice de
[FI]. Si I est l'intersection de la directrice et de
la perpendiculaire passant par F à d', la demi-droite
lieu de J a pour support la parallèle à l'axe
de la parabole passant par I.
 La
figure PBDrt3.fig
ci-contre. La
figure PBDrt3.fig
ci-contre.
On a donc le résultat
suivant :
Le lieu des milieux des cordes
d'une parabole, parallèles à une direction
fixe, est une demi-droite intérieure à la
parabole et parallèle à son axe. Ce lieu
s'appelle le diamètre
conjugué à la direction de
d'.
Remarque :
Le terme de diamètre
provient de la géométrie projective : c'est un
diamètre au sens où le centre de la parabole
est le point à l'infini dans la direction de l'axe.
En ce sens cette demi-droite passe bien par le centre de la
parabole.
|