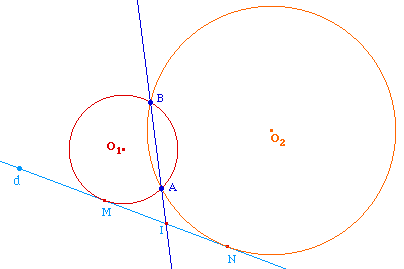
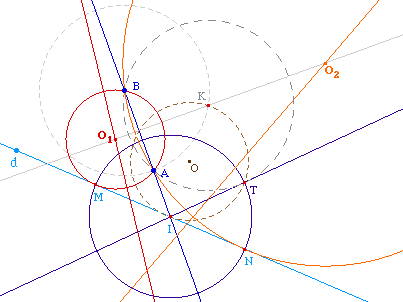
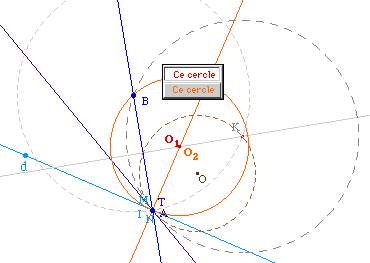
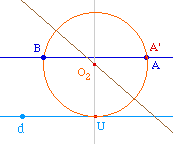
Si la droite (AB) coupe la droite d, leur point d'intersection I est sur l'axe radical des cercles solutions, mais aussi sur la tangente commune à ces deux cercles. Ainsi IM = IN car IM² = IN² = IA.IB.

On peut donc construire les cercles solutions en construisant leur point de contact car la longueur de la tangente IM est la même pour tout cercle de même axe radical (AB) - on dit appartenant au même faisceau de cercle. Il suffit donc d'en construire un et de construire une de ses tangentes issue de I.

Pour pouvoir transformer la figure en macro, il faut construire le cercle intermédiaire à partir des seules données du problème. Ici on a construit le cercle de centre K sur la médiatrice de [AB], en prenant K sur le cerlce de centre B passant par A. Le cercle de diamètre [IK] coupe - classiquement - ce cercle en un point T pour lequel (IT) lui est tangente en T.

Or IT² = IA.IB donc M et N sont l'intersecton de la droite d avec le cercle de centre I passant par T. On trouve les centres en construisant les médiatrices de [AM] et de [AN], ou encore les perpendiculaires à d passant par M et N.

TgtC2P1D.fig ci-contre.

La figure n'est pas terminée.

La macro appliquée à (AB), d, et A renvoie sous A un point A' qui n'existe que si les deux droites sont parallèles. La médiatrice de [AB] coupe d en U. La médiatrice de [A'U] coupe celle de [AB] au centre de l'unique cercle solution.

Comme la construction dépend de l'existence de A', ce cercle n'existe que quand les droites sont parallèles. En particulier, sur le plan algorithmique, ce n'est pas le même cercle qu'un des deux précédents du cas général.