|
|
Soit C un cercle, A et B deux points à l'intérieur du cercle, tels que (AB) ne passe pas par le centre du cercle. Construire un cercle C' passant par A et B et sécant à C selon un de ses diamètres. |
 |
|
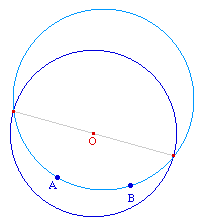
Soit C un cercle, A et B deux points à l'intérieur du cercle, tels que (AB) ne passe pas par le centre du cercle. Construire un cercle C' passant par A et B et sécant à C selon un de ses diamètres.
Lancer la figure ExpPuC1.fig d'expérimentation ci dessus.
Coup de pouce
Solution
Soient C et C' deux cercle et A un point. Construire les droites passant par A interceptant les deux cercles selon des cordes égales.
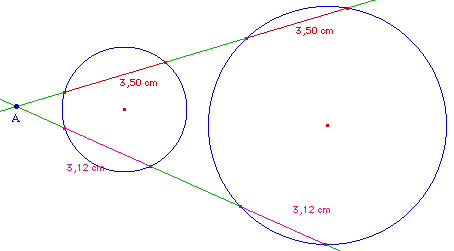
Lancer la figure ExpPuC2.fig d'expérimentation ci-dessus.
Coup de pouce
Solution
![]()
Les coups de pouce
Vous avez probablement connu ces exercices d'application immédiate du théorème de Thalès. Souvenez-vous, on appliquait le sens direct deux fois et le sens réciproque une fois. C'est la même chose ici : prendre par exemple un cercle intermédiaire passant par A et B et faire dans le "Thalès elliptique".
![]()
Phase d'analyse : soit I le milieu des centres des deux cercles. Que peu-t-on dire de J, projeté orthogonal de I sur une droite solution ?
Synthèse : Ainsi J est sur l'intersection d'une droite et d'un cercle, il peut donc y avoir deux solutions.