Rappel du texte

Soient C et C' deux cercle et A un point. Construire les droites passant par A interceptant les deux cercles selon des cordes égales.

Lancer la figure ExpPuC2.fig d'expérimentation

 

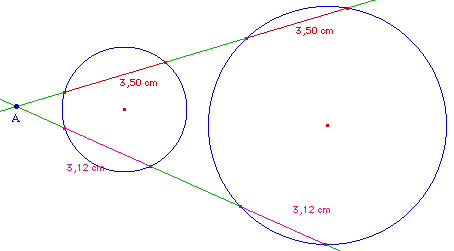
Premier lieu

Soit I le milieu de [OO']. Notons K, K' et J les projections orthogonales respectives de O, O' et I sur une droite solution. Alors J est milieu de [KK'].

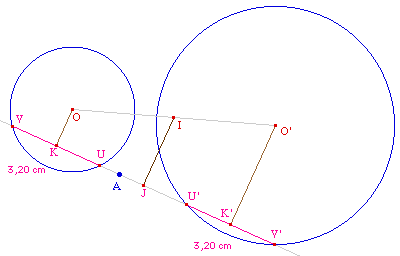
Mais comme UK = U'K', on en déduit de JU = JU' et JV = JV' et donc, en mesure algébrique, on a JU.JV = JU'.JV'. Ainsi J est un point de l'axe radical des deux cercles.

Second lieu

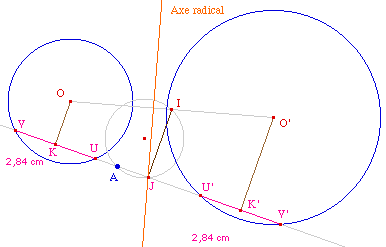
De plus, le triangle AJI, par définition de J, est rectangle et donc J appartient aussi au cercle de diamètre [AI].

Les droites solution sont donc des droites (AJ) où J est l'intersection de l'axe radical des deux cercles, et du cercle de diamètre [AI].

Synthèse

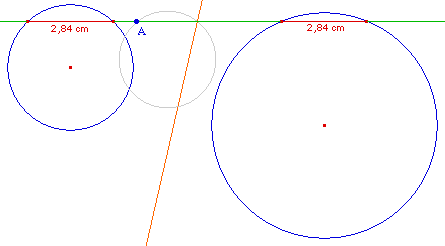
On remarquera que ces droites (AJ) ne sont pas toujours sécantes aux cercles C et C' (ci-dessus il y a clairmeent un point qui ne convient pas). Il en résulte que, pour une Cabri-construction, on prendra soin de construire d'abord l'éventuelle intersection, et ensuite construire, sur ces intersections, les droites effectivement solution.

 

Lancer la figure SolPuC2.fig finale.

Menu général

Retour