[Résultats
généraux] [Axe
radical] [Premières
applications de constructions]
[Problème
d'Appolonius] [Exercices sur
la puissance et les axes radicaux] [Retour
Géométrie 2D]

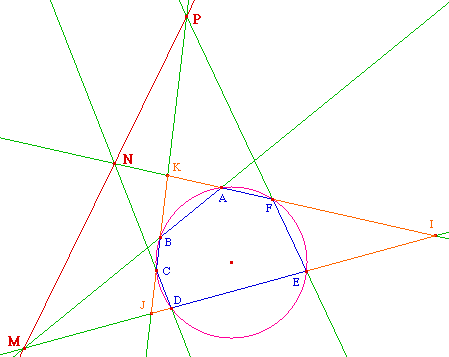
1.a. de I :
1.b. de J :
1.c. de K :
M, A, B alignés :
N, D, C alignés :
P, E, F alignés :
|
|
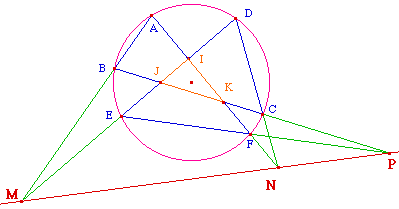
En particulier, mentionnons ce cas particulier, non montré ici, où les points M, N, et M sont alignés sur la droite projective de l'infini, c'est-à-dire le cas où les côté opposés sont parallèles : alors les six points sont encore sur une conique.
|
[Résultats
généraux] [Axe
radical] [Premières
applications de constructions]
[Problème
d'Appolonius] [Exercices sur
la puissance et les axes radicaux] [Retour
Géométrie 2D]