Théorème de
Morley
6.2.B - Complément : les
centres des 27 triangles de
la configuration de Morley
[1 - Théorème
initial] [2 - Les 6 trissectrices
d'un angle - Notations] [3 - Les 27
triangles équilatéraux de Morley]
[4 - Autres triangles
équilatéraux de la configuration ]
[5 - Commentaires et figures
finales]
[7 - Historique et
Références] [Retour
"Grands Classiques"] [Retour
"Géométrie Plane"]
Comme il passe toujours une conique par 5
points (non dégénérée si trois points ne
sont pas alignés), on s'intéresse à
l'équivalent de la cocyclicité de 4 point pour les
coniques : le regroupement de 6 points sur une même conique.
Nous parlerons de "co-conicité" (bon, c'est pas trés
joli)
Les centres de 18 triangles sur 3 coniques
disjointes
Les preuves sont proposées plus loin
sur la page, mais si on veut observer
avec Cabri que 6 points sont sur une même conique on
peut construire la conique qui passe par 5 de ces points et
vérifier, par les propriétés de Cabri, que le
dernier point est bien sur la conique construite.
Le premier résultat est entièrement contenu dans la
figure suivante :
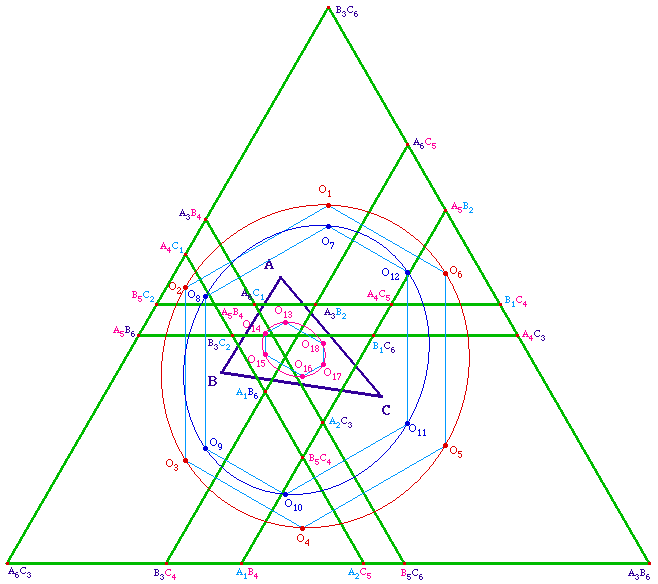
Les centres de 18 triangles
équilatéraux sur 3 coniques - De plus les trois
hexagones associés ont leurs cotés
parallèles.
On observera que les centres des trois coniques (non tracés
ici) sont alignés.
 MRLCCM1.fig (figure
intermédiaire)
MRLCCM1.fig (figure
intermédiaire)
Notations retenues pour les
centres
Centre
|
Triangle
équilatéral
|
Centre
|
Triangle
équilatéral
|
O1
|
B1C4
B3C6
B5C2
|
O10
|
B1C2
B3C4
B5C6
|
O2
|
A4C1
B5C2
A5B4
|
O11
|
B3C4
A3B6
A6C5
|
O3
|
A2C5
A4C1
A6C3
|
O12
|
A2C1
A4C3
A6C5
|
O4
|
A1B4
A2C5
B5C4
|
O13
|
B1C2
A3B2
A6C1
|
O5
|
A1B4
A3B6
A5B2
|
O14
|
A1B6
A3B2
A5B4
|
O6
|
B1C4
A5B2
A4C5
|
O15
|
A2C1
B3C2
A1B6
|
O7
|
A4C3
B3C6
B5C2
|
O16
|
B1C6
B3C2
B5C4
|
O8
|
A1B2
A3B4
A5B6
|
O17
|
A1B2
A2C3
B1C6
|
O9
|
A3B4
A6C3
B5C6
|
O18
|
A2C3
A4C5
A6C1
|
Preuve
L'angle (géométrique)
B5C2 O1 B1C4
vaut 2Pi/2. Or il est clair, puisque B5C2
A5B4 A4C1 et
B1C4 A5B2 A4
C5 sont tous deux équilatéraux, que c'est
aussi l'angle de O2O1O6. On
montrerait de même les angles
O1O6O5,
O6O5O4,
O5O4O3,
O4O3O2 et
O3O2O1 font eux aussi tous 2Pi/3. Il
en résulte que l'hexagone
O1O2O3O4O5O6
a ses côtés opposés
parallèles.
Or on sait que c'est un
cas particulier du
théorème de
Pascal dit de "l'hexagramme mystique"
pour que ces 6 points soient sur une même conique.
En considérant au départ le
triangle équilatéral B3C6
A5B6 A4C3 et deux
associés, on montre de la même manière que les
points l'hexagone
O7O8O9O10O11O12
a aussi ses côtés opposés parallèles et
qu'il est donc lui aussi inscrit dans une conique.
Par ailleurs, on notera que les
côtés correspondants sont respectivement
parallèles. Par exemple (O1O2) //
(O7O8) car ces droites sont des hauteurs de
triangles équilatéraux de même base
(B3C6 A3B6).
Cet argument des hauteurs convient bien
aussi pour les six derniers points, de O13 à
O18. Par exemple il est clair que (O13
O14) // (O1 O2) car O13
et O14 sont sur la hauteur de deux triangles
équilatéraux issues de A3B2 donc
ils forment une droite perpendiculaire à
(A4C1 A2C5) par exemple.
Ainsi, par parallèlisme au premier hexagone, il est
évident que les points O13 à O18
sont inscrits eux aussi sur une même conique.
Les centres de 9 derniers triangles
 MRLCCM2.fig (figure finale -
temporairement)
MRLCCM2.fig (figure finale -
temporairement)
On ajoute les centres O19 à O27 qui
sont ceux de 9 triangles formant une partition des 27 points (la
partition retenue dans la présentation de la page 3). On
notera que les points O19 à O24 sont sur
les côtés de l'hexagone O1...O6.
C'est évident par les arguments de hauteur par exemple. De
même O19 est sur (O8 O9),
O20 sur (O7 O8) etc ... nous avons
donc de nombreux parallélogrammes comme
O2O20O8O19 mais aussi
O2O3O9O19 ou encore
O3O4O22O9 et donc
O2O4O22O19. Et ainsi de
suite, nous ne nous attarderons pas sur les trés nombreux
parallélogrammes ainsi présents dans cette figure, leur
existence est évidente, et nous les utiliserons
spontanément quand cela sera utile.
On remarquera par contre que les points O19 à
O24 ne sont pas six points d'une même conique.
Notation des points
Centre
|
Triangle
équilatéral
|
O19
|
A6C1
A3B4
B5C2
|
O20
|
B3C2
A4C1
A5B6
|
O21
|
A1B6
B3C4
A2C5
|
O22
|
A2C3
A1B4
B5C6
|
O23
|
A5B2 B1C6
A4C3
|
O24
|
A6C5
A3B2
B1C4
|
O25
|
A1B2
B1C2
A2C1
|
O26
|
A4C55
A6B4
B5C4
|
O27
|
A3B6
B3C6
A6C3
|
Quelques coniques contenant ces
points
Parmi tous ces points, supprimons ceux qui intervienent
déjà dans la classification de la page
précédente, c'est-à-dire ceux qui sont sur les
médiatrices du triangle ABC. Ce sont les centres O1
- O3 - O5 sur la première conique, puis
O8 - O10 - O12 sur la
deuxième conique et O14 - O16 -
O18 sur la troisième conique. Utilisons les
parallèlogrammes précédents pour chercher des
regroupement de 6 points sur une même conique :
a - Trois coniques passant par
O25
En reprenant la figure
générale, il est clair en considérant les
triangles dont ils sont le centre d'une par que
O19O2O15O25 est un
parallélogramme et d'autre part que
O2O20O25O13 est aussi un
parallèlogramme. Autrement dit, non seulement les six points
O19, O2, O20, O15,
O25, O13 sont sur une même conique, par
le théorème de Pascal, mais de plus ce sont des
diamètres de cette conique puisque les trois segments
[O19 O15], [O2
O25], [O20 O13] ont
même milieu.
Chacun pour reprendre ce raisonnement pour
les autres coniques proposées ci-dessous, y compris en b et c
donnés pour le plaisir des yeux.
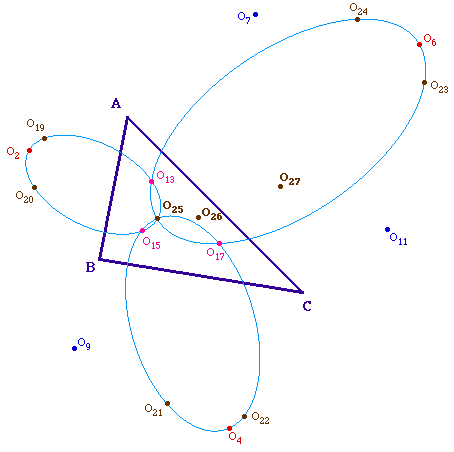
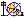 MRLCCM3.fig (figure
intermédiaire)
MRLCCM3.fig (figure
intermédiaire)
a - Trois coniques passant par
O26
Par exemple ici, comme
détaillé ci-dessus,
O19O2O4O22 est un
parallèlogramme, de même pour
O26O2O9O22 ce qui assure
à nouveau que les six points sont sur une même conique
et que l'on a affaire à trois diamètres de la
conique.
 MRLCCM4.fig (figure
intermédiaire)
MRLCCM4.fig (figure
intermédiaire)
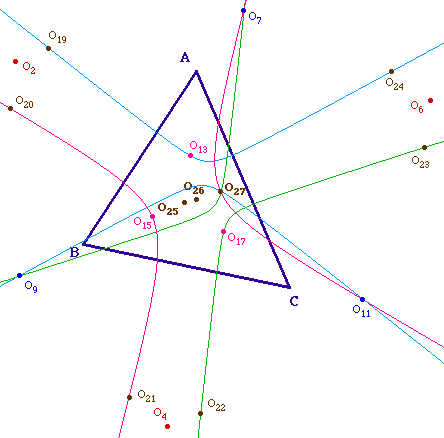
c - Trois coniques passant par
O27
L'illustration suivante est aussi celle
des limites de l'exploration en vue de
conjecture avec un logiciel de
simulation (ie non associé à un calcul formel par
exemple). En effet, pour ces hyperboles, l'appartenance du dernier
point à l'hyperbole est sensible à la construction de
l'hyperbole. Par exemple, pour une même configuration de points
:
Pour la conique passant
par
|
le sixième
point
|
pour le test
d'appartenance de Cabri
|
O20 - O15 - O21
- O7 - O11
|
O27
|
n'est pas sur la conique
|
O7 - O27 - O11
- O21 - O15
|
O20
|
est sur la conique
|
Justifions précisément la "co-conicité" de
ces points - par exemple pour la conique bleue, les autres se
traitant de manière identique par permutation circulaire.
O19O9O11O24 est un
parallèlogramme car les côtés
[O9O19] et
[O11O24] sont paralléles et de
même longueur (égale par exemple à
O2O3). Par ailleurs
(O19O13) // (O27O11) car
toutes deux perpendiculaires à (B3C6
A6B3). De même
(O13O24) // (O9O27) comme
perpendiculaires à (B3C6
A3B6). Ainsi la symétrie centrale de
centre le milieu de [O19O11]
transforment O9 en O24, envoie aussi - par
parallélisme - O13 sur O27. Cela suffit
pour montrer tout d'abord que l'hexagone
O13O19O9O27O11O24
a ses côtés deux à deux parallèles dont
est inscrit dans une conique, ensuite que ces six points sont les
extrémités de trois diamètres de cette
conique.
 MRLCCM5.fig (figure
intermédiaire)
MRLCCM5.fig (figure
intermédiaire)
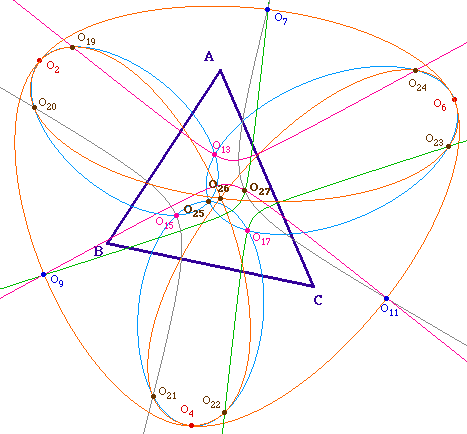
c - Figure regroupant les 9
coniques
Chacun remarquera les symétrie de
construction, en particulier dans l'utilisation des 9 derniers
centres dans ces constructions de coniques. Il est clair que d'autres
groupes de 6 points sur une même conique existent : plus
précisément, en considérant les 27 centres, il
ne serait pas surprenant que l'on trouve des coniques telles que par
chaque sommet il en passe 3, comme pour les triangles
équilatéraux : en regroupant ces 9 coniques avec les 3
du départ, c'est déjà vrai pour les centres
O2, O4, O6, O13,
O15, O17, O25, O26,
O27. Ces pages sont donc transitoires : elles ont
été mises en ligne pour succiter la curiosité
... l'auteur n'ayant plus actuellement le loisir de poursuivre ...
mais il "y retournera" dès que possible.
 MRLCCM6.fig (figure
intermédiaire )
MRLCCM6.fig (figure
intermédiaire )
[1 - Théorème
initial] [2 - Les 6 trissectrices
d'un angle - Notations] [3 - Les 27
triangles équilatéraux de Morley]
[4 - Autres triangles
équilatéraux de la configuration ]
[5 - Commentaires et figures
finales]
[7 - Historique et
Références] [Retour
"Grands Classiques"] [Retour
"Géométrie Plane"]
 Menu général
Menu général

![]() MRLCCM1.fig (figure
intermédiaire)
MRLCCM1.fig (figure
intermédiaire)

![]() MRLCCM1.fig (figure
intermédiaire)
MRLCCM1.fig (figure
intermédiaire)

![]() MRLCCM2.fig (figure finale -
temporairement)
MRLCCM2.fig (figure finale -
temporairement)
![]() MRLCCM3.fig (figure
intermédiaire)
MRLCCM3.fig (figure
intermédiaire)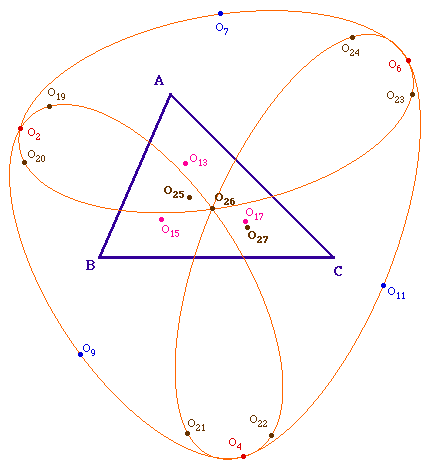
![]() MRLCCM4.fig (figure
intermédiaire)
MRLCCM4.fig (figure
intermédiaire)

![]() MRLCCM5.fig (figure
intermédiaire)
MRLCCM5.fig (figure
intermédiaire)

![]() MRLCCM6.fig (figure
intermédiaire )
MRLCCM6.fig (figure
intermédiaire )