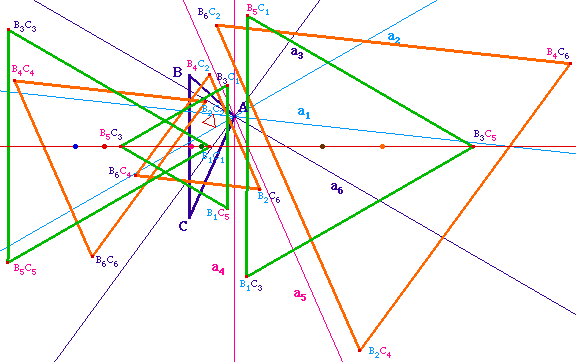
Les centres des 6 triangles équilatéraux sont alignés sur la médiatrice de [BC]
![]() MRLaaC.fig
ou la macro TRtypeaa.mac
MRLaaC.fig
ou la macro TRtypeaa.mac
6.2 - Complément : les centres des triangles de Morley

Les centres des 6 triangles équilatéraux sont alignés sur la médiatrice de [BC]
![]() MRLaaC.fig
ou la macro TRtypeaa.mac
MRLaaC.fig
ou la macro TRtypeaa.mac
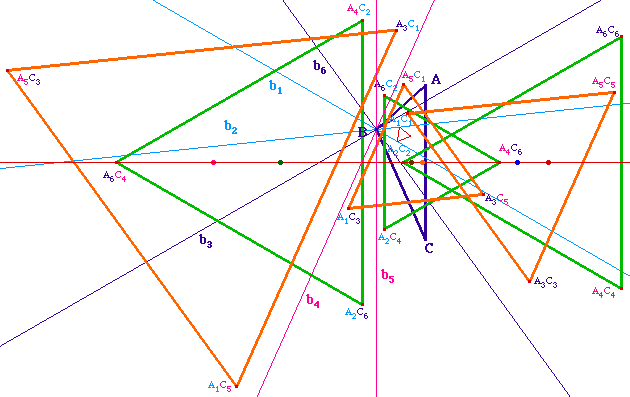
Les centres des 6
triangles équilatéraux sont alignés sur la
médiatrice de [AC]
![]() MRLbbC.fig
ou la macro TRtypebb.mac
MRLbbC.fig
ou la macro TRtypebb.mac
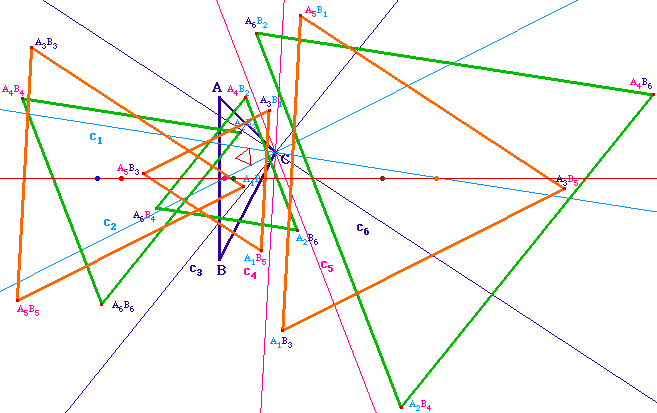
Les centres des 6
triangles équilatéraux sont alignés sur la
médiatrice de [AB]
![]() MRLccC.fig
ou la macro TRtypecc.mac
MRLccC.fig
ou la macro TRtypecc.mac
du centre |
de [BC] |
de [AC] |
de [AB] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
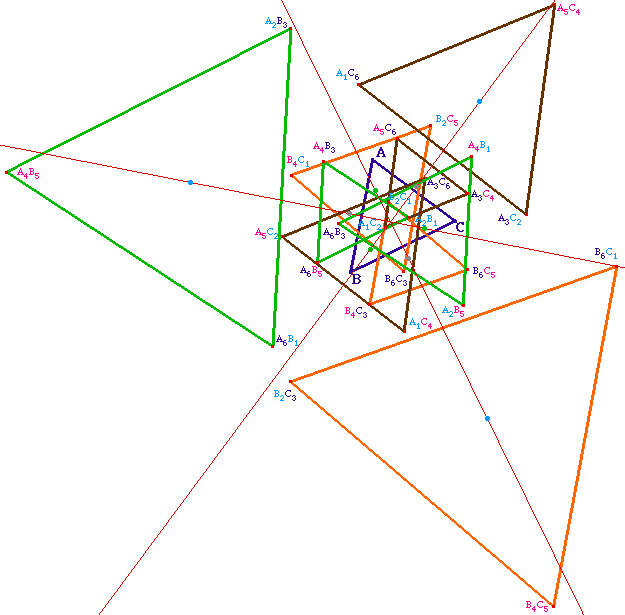
Les centres des 9 triangles
équilatéraux suivants sont aussi alignés sur les
médiatrices de ABC
![]() MRL9abcC.fig
ou la macro TRtype9S.mac
MRL9abcC.fig
ou la macro TRtype9S.mac
du centre |
de [BC] |
de [AC] |
de [AB] |
|
|
|
|
|
|
|
|
|
|
|
|
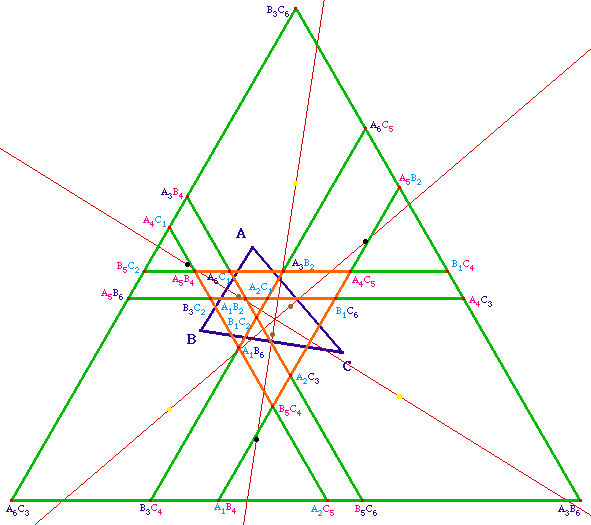
Les centres d'une des partitions de la
configuration de Morley sont aussi alignés sur les
médiatrices de ABC
![]() MRL9abcC.fig
ou la macro TRtypeCM.mac
MRL9abcC.fig
ou la macro TRtypeCM.mac
du centre |
de [BC] |
de [AC] |
de [AB] |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
On peut regrouper toutes ces observations dans une seule macro qui renvoie les 36 centres de ces triangles équilatéraux. Pour utiliser cette macro, on remarquera qu'avec la couleur des centres et la médiatrice qui le contient, on repère facilement le triangle dont un point donné est le centre.
|