L'existence de ce centre M a été mis en évidence en 1967 par Peter Yff qui en a calculé ses coordonnées barycentriques dans le repère (A, B, C) :

sin(A)/sin(A/3)
sin(B)/sin(B/3)
sin(C)/sin(C/3)

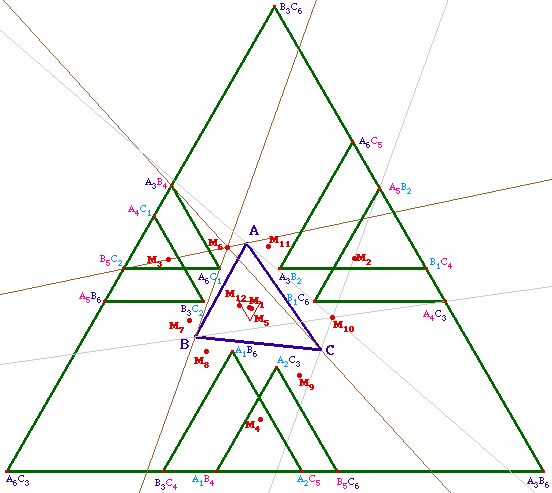
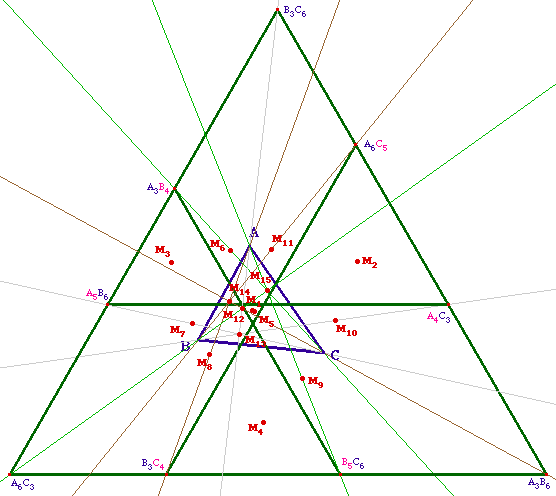
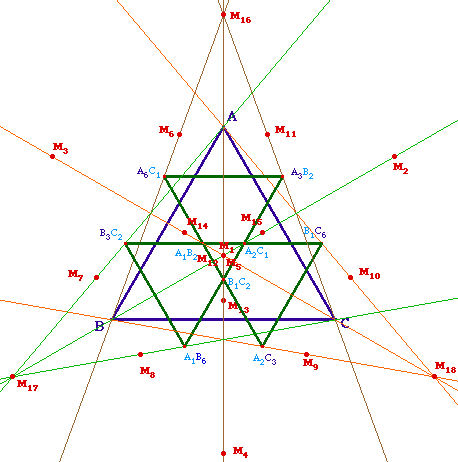
Si on observe la figure ci-contre on s'aperçoit que le triangle de Morley central a ses sommets sur des trissectrices issues de chacun des trois sommets du triangle de départ.

Or on a vu dans la page 4A qu'il y a 18 triangles, dans la configuration de Morley, qui sont construits ainsi. On peut donc s'intéresser à d'éventuelle concourance de droites pour les 17 autres triangles. Observons ce qu'il en est :

On peut facilement conjecturer, avec Cabri, et ses outils de vérification, que les 4 triangles construit avec les trisectrices des angles supplémentaires à ceux du triangle ont aussi un centre de Morley :

Par exemple, pour le triangle A₄C₅ B₁C₄ A₅B₂, les droites (A B₁C₄), (B A₄C₅) et (C A₅B₂) sont concourantes en un point noté M₂ sur l'illustration ci-contre (M₅ est le centre de Morley du triangle B₅C₄ A₄C₅ A₅B₄).

MRLCtrA.fig