[2.B - Etoiles - Triangles équilatéraux] [2.C - Autres propriétés des étoiles]

Les 6 trisectrices d'un angle

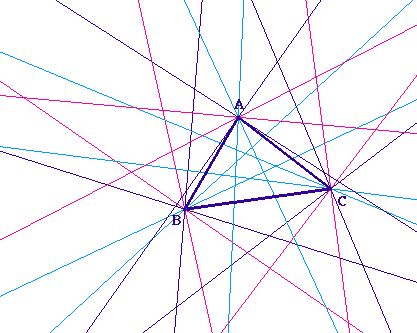
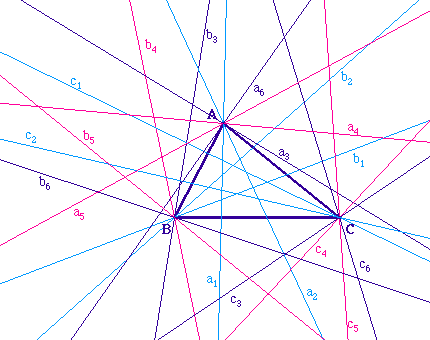
	Le théorème de base a utilisé la trisection des angles géométriques d'un triangle, comme ci-contre. Nous nous proposons, dans les pages suivantes d'explorer les possibilités de généralisation en étendant la trisection aux angles de droites puis de vecteur. La trissectrice est constuite naturellement par Cabri en prenant le tiers d'un angle, de manière analytique. Rappelons que cette opération n'est pas réalisable en général à la règle et au compas.
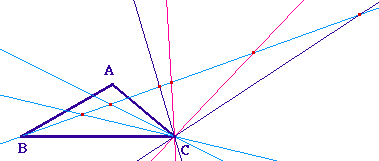
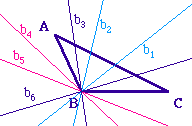
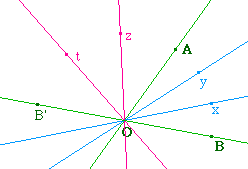
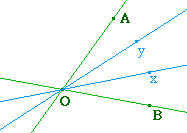
	En comparaison avec les "bissectrices extérieures", une première extension est de considérer les angles de droite, et donc de faire la trisection du supplémentaire. Par exemple ci-contre, [Oz) et [Ot) sont les trissectrices intérieures de l'angle géométrique AOB'. En particulier yOz vaut 60°. De même, pour l'angle de droite (Ot, Ox).
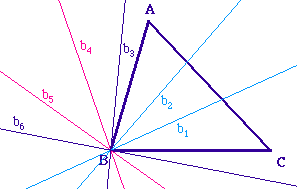
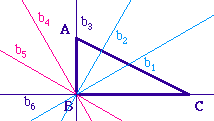
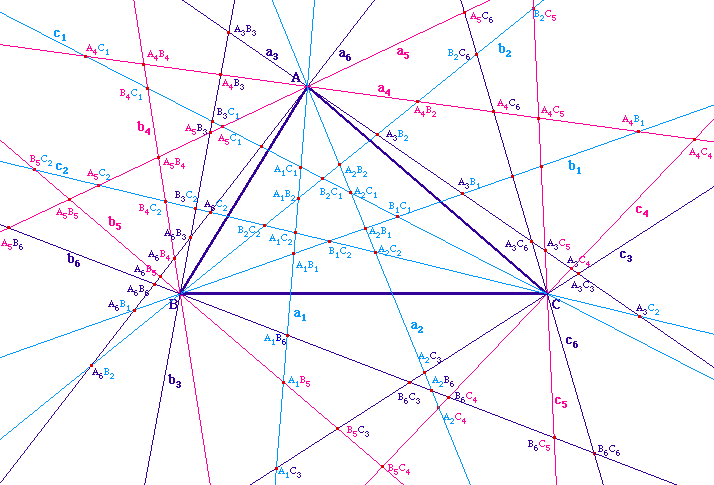
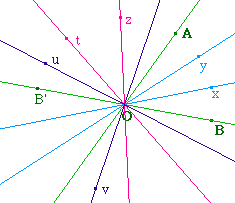
	Si on veut s'affranchir des angles géométriques, il est plus intéressant de considérer l'angle de vecteur (OB, OA). Sa mesure étant définie à 2 Pi près, les trisectrices se répartissent modulo 2 Pi/3. On dispose donc de 6 trissectrices pour un angle. En particulier, sur l'illustration ci-contre, les angles géométriques yOu et xOv valent chacun 120°. Trisect.fig

Une autre présentation consiste à traiter directement des angles de droites : les droites d = (OA) et d' = (OB) font un angle de droite a = (d, d') ou -a = (d', d) modulo Pi. Soit en résolvant a = 3x et -a = 3x modulo Pi, on obtient deux fois trois solutions, soit 6 droites trissectrices de d et d', avec les relations d'angles en elles comme indiqué ci-dessus.

Les trisectrices d'un triangle

Les notations retenues

Elles ne sont peut-être pas typographiquement les plus efficaces - 4 caractères pour les points alors que 3 aurait pu suffir - mais la notation de ces pages permet de repérer immédiatement les types de trissectrices rencontrées par le nom d'un point.

Pour les trisectrices

Avec ces notation il résulte que les trissectrices d'un même angle d'indices 1 - 3 - 5 ou d'indices 2 - 4 - 6 forment des angles de 60°, ce qui rentre dans le cadre des étoiles définies à la page suivante.

Pour leurs intersections

On notera A_iB_j (respectivement A_iC_j, B_iC_j) l'intersection des droites a_i et b_j (respectivement a_i et c_j, b_i et c_j). Ce qui donne :

 

Illustration en proche banlieue

 

  Notation.fig (pouvant servir pour aborder les prolongements)

Le contenu des pages 2.B. et 2.C.

On montre en 2.B - dans un cadre plus général - que les intersections des trissectrices produisent 36 triangles équilatéraux. On utilise simplement les outils de cocyclicité et de puissance d'un point par rapport à un cercle. Ensuite, en 2.C. on évalue la direction des côtés des triangles et on montre que sur ces 36 triangles, 18 sont parallèles aux trissectrices de ABC, à raison de 6 par groupe de trissectrices issues de A, B et C. Les pages du chapitre 3 sont consacrées à des illustrations de ces propriétés.

[2.B - Etoiles - Triangles équilatéraux] [2.C - Autres propriétés des étoiles]

Menu général