|
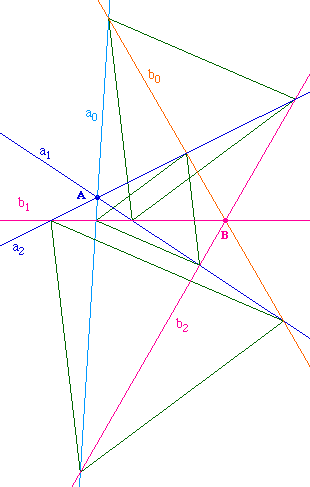
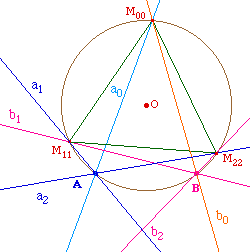
Par des arguments de cocyclicité, le cercle
circonscrit à M00, M11, et A
contient B. DE même, le cercle circonscrit à
M00, Bet M22 contient A.
Cela signifie que ces 5 points sont cocycliques sur un
cercle de centre O.
En angle de droites, on a :
(AM22, AM00) = (a2, a0) = Pi/3
[Pi].
Et donc en angle de vecteurs :
(OM22, OM00) = 2Pi/3
[2Pi].
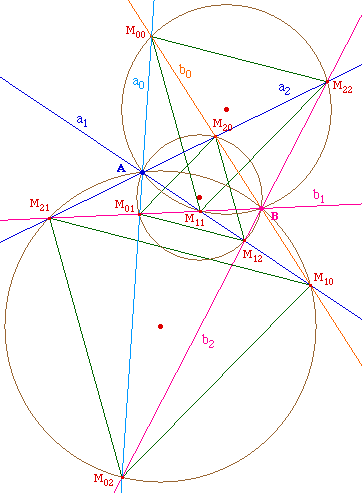
De même pour les autres côtés, donc
le triangle admet une rotation d'angle2¼/3 comme
isométrie : c'est un triangle
équilatéral (de plus direct).
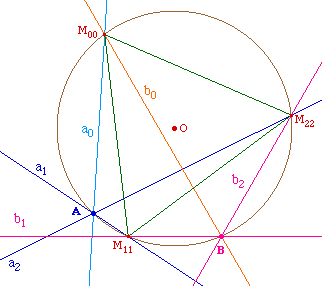
On pourrait aussi raisonner directement sur les angles
de droites : le triangle ayant ses trois angles de droites
égaux à Pi/3, il est alors
nécessairement équilatéral.
|