|
 Etoile02.fig
Etoile02.fig
|
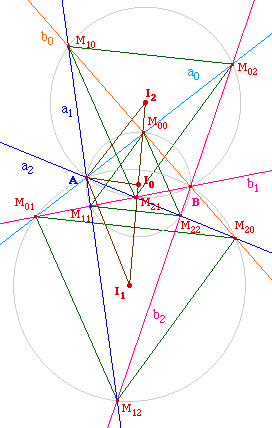
Considérons la similitude directe qui envoie le
triangle M00M11M22 sur le
triangle M02M10M21 en
envoyant M00 sur M10 et M22
sur M02. On sait que son centre est l'autre point
d'intersection des cercles circonscrits à
M00M22B et
M10M02B car B est l'inersection des
droites (M00M10) et
(M22M02). Cet autre point
d'intersection est A et la similitude est alors d'angle
M00AM10 soit de Pi/3.
De même, on passe de
M01M12M20 à
M00M11M22 par une autre
similitude de centre A et d'angle Pi/3.
Ainsi, en notant I0, I2 et
I1 les centres des trois triangles, on passe de
l'un à l'autre par une similitude de centre A et
d'angle Pi/3 ou 2Pi/3 (ou leurs opposés).
Par exemple, dans l'illustration ci-contre où
I0 est entre I1 et I2, les
angles en A des triangles I1AI0,
I0AI2 et I1AI2
ont tous même sinus car l'angle vaut Pi/3 ou
2Pi/3.
En notant Rk = AIk, les rayons des
cercles circonscrits aux triangles, le fait que l'aire du
triangle AI1I2 (dans cette
illustration) soit la somme des aires des triangles
AI0I2 et AI1I0
permet d'écrire - avec la formule des sinus - que
:
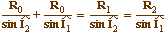 soit
soit 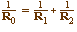
On retiendra que l'inverse du plus
petit rayon est la somme des inverses des deux autres.
Il en est de même pour les côtés des
triangles, par exemple (dans cette illustration) :
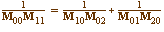
|
