|
|
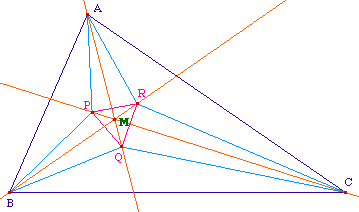
L'existence de ce centre M a été mis en évidence en 1967 par Peter Yff qui en a calculé ses coordonnées barycentriques dans le repère (A, B, C) :
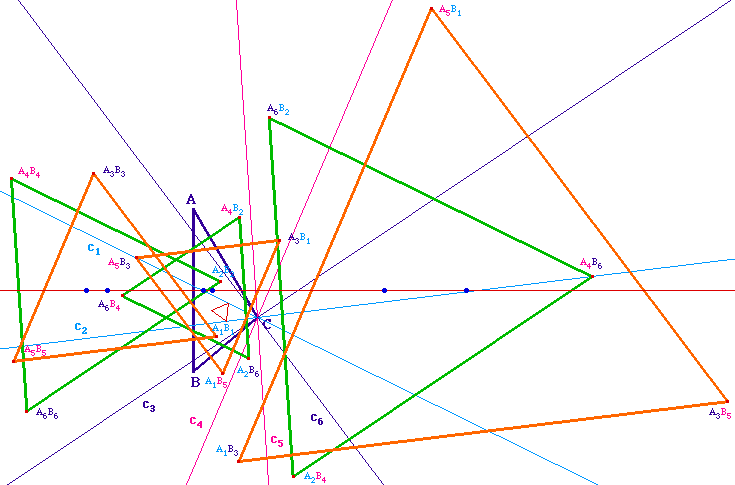
La page 6.1 met en évidence - toujours expérimentalement - l'existence de 17 autres tels centres de Morley et s'essaie à quelques propriétés relatives à ces points. |