Théorème de Morley

6.1.B - Compléments : les centres de Morley

 [6.1.A - Définition des centres de Morley] [6.2 - Les centres des triangles de Morley]  

 [1 - Théorème initial] [2 - Les 6 trissectrices d'un angle - Notations] [3 - Les 27 triangles équilatéraux de Morley]
[4 - Autres triangles équilatéraux de la configuration ] [5 - Commentaires et figures finales]
[7 - Historique et Références] [Retour "Grands Classiques"] [Retour "Géométrie Plane"]

 

Cette page ne contient pas (pas encore) de propriétés particulières sur les centres de Morley, mais se propose seulement d'illustrer quelques conséquences élémentaires propre à leur existence.

 

Par construction ces centres sont, par paires, alignés avec l'un des sommets du triangle

 

 

MRL18CT2.fig

 

On se souvient aussi (illustration de la page 2 sur les trissectrices), que quand le triangle ABC a un angle droit, deux des six trissectrices sont confondues avec les côtés de l'angle droit. Il en résulte que plusieurs centres de Morley (6 dans chaque cas) sont alors confodus avec le sommet. Ainsi, on a :

 

 

 

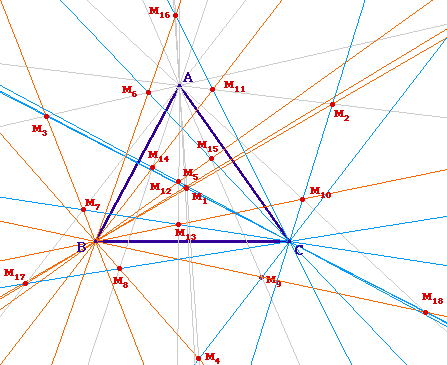
Enfin, avant de chercher quelques propriétés relatives à ces centres, il peut être intéressant d'observer un autre cas particulier : celui du triangle équilatéral. Les centres de Morley sont soit confondus (sur le centre du cercle circonscrit), soient cocycliques sur un cercle centré au centre du cercle circonscrit au triangle.

 

Mais cela n'augure pas pour autant de propriétés sur ces points : par exemple les six points cocycliques sur le cercle bleu ne sont pas sur une même conique dans le cas général.

 

 [6.1.A - Définition des centres de Morley] [6.2 - Les centres des triangles de Morley]

 

 [1 - Théorème initial] [2 - Les 6 trissectrices d'un angle - Notations] [3 - Les 27 triangles équilatéraux de Morley]
[4 - Autres triangles équilatéraux de la configuration ] [5 - Commentaires et figures finales]
[7 - Historique et Références] [Retour "Grands Classiques"] [Retour "Géométrie Plane"]

 

Menu général