Théorème de
Morley
6.2.C - Complément :
Propriétés des coniques
précédentes
[1 -
Théorème initial] [2
- Les 6 trissectrices d'un angle - Notations] [3
- Les 27 triangles équilatéraux de Morley]
[4 - Autres triangles
équilatéraux de la configuration ]
[5 - Commentaires et figures
finales]
[7 - Historique et
Références] [Retour
"Grands Classiques"] [Retour
"Géométrie Plane"]
Rappel du résultat
précédent : 9 coniques regroupant chacune 6 centres
de triangles équilatéraux, et concourantes par 3 en les
centres O25, O26, O27
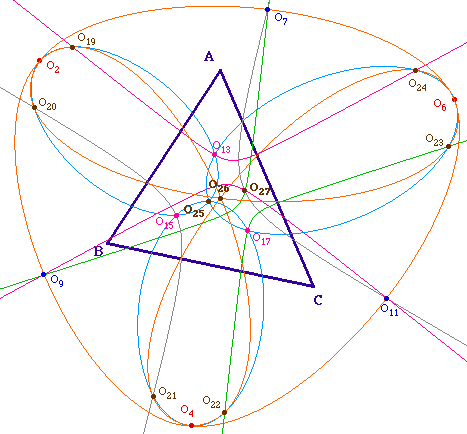
 MRLCCM6.fig (figure
intermédiaire)
MRLCCM6.fig (figure
intermédiaire)
Les centres de ces 9 coniques
Ils sont - eux aussi ! - trois par
trois alignés sur les médiatrices du triangle ABC de
départ.
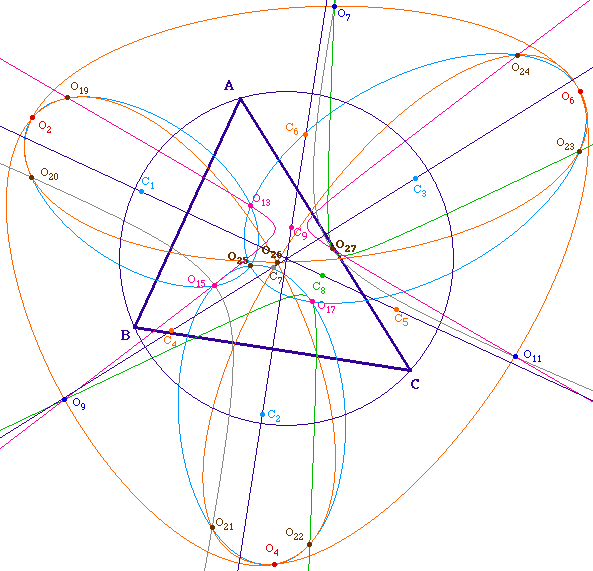
 MRLCCM7.fig (figure
d'illustration )
MRLCCM7.fig (figure
d'illustration )
Remarque : ce
résultat est une Cabrti-conjecture au moment de la
rédaction de cette page. Il sera montré
ultérieurement.
Sur les axes focaux de ces coniques (autre
Cabri conjecture)
Les trois coniques passant par
O25 ont leurs axes focaux concourants (en vert
ci-dessous).
Les trois coniques passant par O26 ont leurs axes focaux
orthogonaux aux précédents (en rose
ci-dessous).
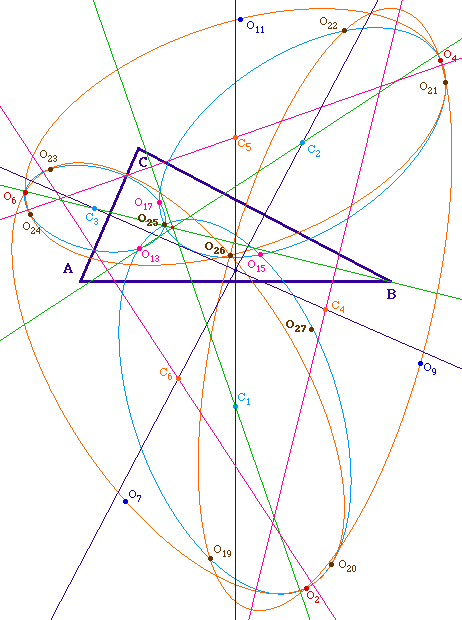
 MRLCCM8.fig (figure
d'illustration )
MRLCCM8.fig (figure
d'illustration )
Remarques :
Pour ce qui est des hyperboles, on observerait
que les axes focaux des hyperboles de centre C7 et
C8 sont parallèles à ceux des ellipses de
centre C3 et C1 respectivement ou ceux des
ellipses de centre C4 et C5, selon la
configuration. Celle de centre C9 a un axe focal
"instable" dans cette figure (possiblement due simplement à la
macro "Axe focal d'hyperbole" qui n'applique mal de la situation
particulière rencontrée ici - les six points
étant des diamètres). Il est perceptivement assez clair
qu'il semble être parallèle à l'axe focal de
l'ellipse centrée en C2 ou C6, mais en
pratique il n'est jamais parallèle. Cela rappelle à la
prudence quant à l'observation sur des figures relativement
complexes ...
Autres illustrations du fait que les six
points de chaque conique
forment trois diamètres (pour le plaisir des yeux)
Par exemple ci-dessous, O25 est centre d'une
homothétie qui envoie O2O4O6
sur C1C2C3. On retrouve par exemple
que - en vecteur - O19O22 =
O2O4.
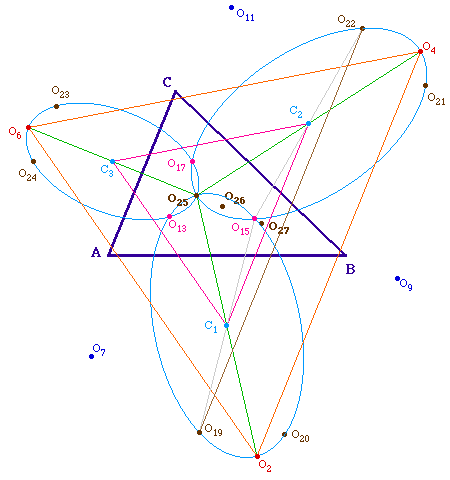
 MRLCCM9.fig (figure
d'illustration )
MRLCCM9.fig (figure
d'illustration )
Les propriétés sont identiques pour les deux autres
triplets de coniques, avec les mêmes remarques :
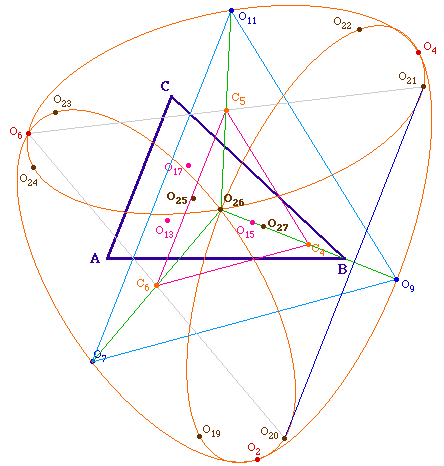
 MRLCCMa.fig (ici illustration de
O20O21 = O7O11)
MRLCCMa.fig (ici illustration de
O20O21 = O7O11)
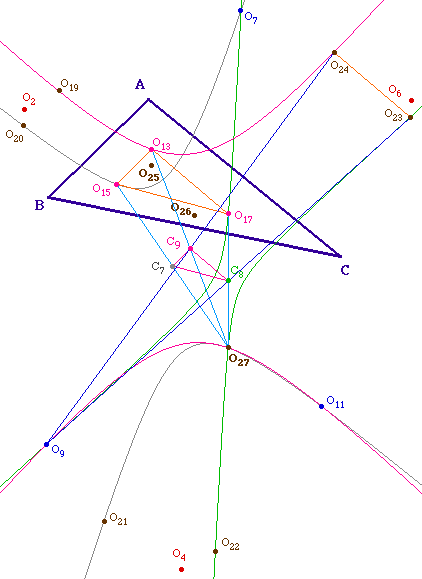
 MRLCCMb.fig (ici illustration de
O23O24 = O17O13)
MRLCCMb.fig (ici illustration de
O23O24 = O17O13)
[1 -
Théorème initial] [2
- Les 6 trissectrices d'un angle - Notations] [3
- Les 27 triangles équilatéraux de Morley]
[4 - Autres triangles
équilatéraux de la configuration ]
[5 - Commentaires et figures
finales]
[7 - Historique et
Références] [Retour
"Grands Classiques"] [Retour
"Géométrie Plane"]
 Menu général
Menu général

![]() MRLCCM6.fig (figure
intermédiaire)
MRLCCM6.fig (figure
intermédiaire)
![]() MRLCCM6.fig (figure
intermédiaire)
MRLCCM6.fig (figure
intermédiaire)
![]() MRLCCM7.fig (figure
d'illustration )
MRLCCM7.fig (figure
d'illustration )
![]() MRLCCM8.fig (figure
d'illustration )
MRLCCM8.fig (figure
d'illustration )

![]() MRLCCM9.fig (figure
d'illustration )
MRLCCM9.fig (figure
d'illustration )
![]() MRLCCMa.fig (ici illustration de
O20O21 = O7O11)
MRLCCMa.fig (ici illustration de
O20O21 = O7O11)

![]() MRLCCMb.fig (ici illustration de
O23O24 = O17O13)
MRLCCMb.fig (ici illustration de
O23O24 = O17O13)