Axe radical de deux cercles
 [Résultats généraux] [Premières applications de constructions] [Problème d'Appolonius]
[Théorème de Pascal] [Exercices sur la puissance et les axes radicaux] [Retour Géométrie 2D]

 

Dans la suite, les cercles considérés sont non concentriques. L'un des deux peut être réduit à un point.

 

Définition

On considère deux cercles C(O, R) et C'(O', R') avec O et O' distincts. L'ensemble des points M de même puissance par rapport aux deux cercles vérifie :

PC(M) = MO2 - R2 = PC'(M) = MO'2 - R'2, soit MO2 - MO'2 = R2 - R'2

C'est donc une ligne de niveau de type MA2 - MB2. On sait que c'est une droite orthogonale à la droite des centres. Cette droite s'appelle l'axe radical de C et C'.

C'est la droite passant par K défini par

L'axe radical (en dehors des parties intérieures aux cercles) est aussi l'ensemble des points desquels on peut mener des segments tangents de même longueur.

Remarque : Si l'un des deux rayons est nul, par exemple R' = 0, on conserve l'expression d'axe radical en parlant d'axe radical d'un cercle et d'un cercle point.
On notera qu'une tangente commune aux deux cercles coupe l'axe radical au milieu du segment reliant les deux points de contact (ci dessus N est milieu de [QQ'].

Si les cercles sont sécants - ou tangents - l'axe radical passe par tout point commun aux deux cercles :

Lancer la figure AxeRD01.fig précédente.

Position de l'axe radical

Il est facile de voir que, si les cercles sont disjoints, l' axe radical :

- coupe le segment [OO'] si les cercles sont extérieurs l'un de l'autre.
- ne coupe pas ce segment [OO'] si un cercle est intérieur à l'autre.

 

Construction de l'axe radical de deux cercles

 

 

La figure AxeRD02.fig
ou
 la macro AxeRad.mac.

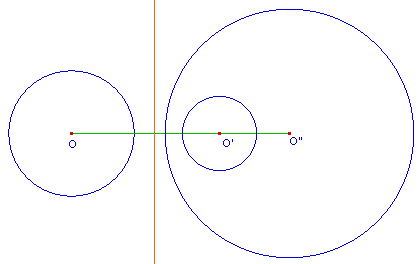
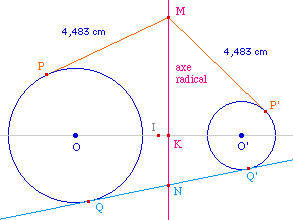
Obtenir une construction générale c'est en particulier obtenir une construction quand les cercles sont disjoints qu'ils soit extérieurs l'un à l'autre ou que l'un soit contenu dans l'autre. Comme on construit trivialement l'axe radical de deux cercles sécants par la droite de leur intersection, il suffit de construire un cercle qui soit sécant à deux cercles donnés (non concentriques) dans tous les cas.

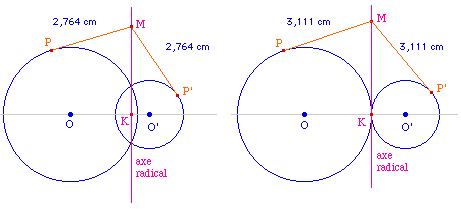
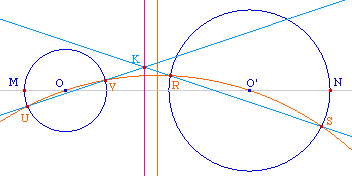
Dans Cabri, l'intersection d'un cercle et d'une droite oriente la droite. Ainsi, si on construit l'intersection des deux cercles avec l'axe des centres, le segment [MN] ci-dessus sera toujours le segment joignant les intersections des cercles avec (OO') mais extérieures à [OO']. Un cercle passant par O et O', et de rayon MN ainsi construit coupe toujours les deux cercles, y compris quand l'un est contenu dans l'autre, puisqu'il est de rayon R+R'+OO'.

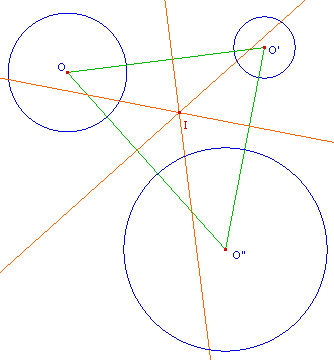
Dans ce cas (UV) est l'axe radical du premier cercle avec ce cercle intermédiaire, (RS) du second cercle avec le cercle intermédiaire. L'intersection K de ces deux axes radicaux appartient donc à l'axe radical des deux cercles donnés.

Cette construction utilise en fait la notion de :

Centre radical de trois cercles

Les axes radicaux de trois cercles de centres non alignés concourrent en un point appelé centre radical des trois cercles.

CentreRD.fig.

Cas particuliers de l'alignement des centres

Alors les axes radicaux sont parallèles ...

... ou confondus.

Exemple

On reconnaîtra l'orthocentre d'un triangle comme le centre radical des trois cercles de diamètres les côtés du triangle.

OrthoAxRD.fig

 

 [Résultats généraux] [Premières applications de constructions] [Problème d'Appolonius]
[Théorème de Pascal] [Exercices sur la puissance et les axes radicaux] [Retour Géométrie 2D]

 

Menu général