 |
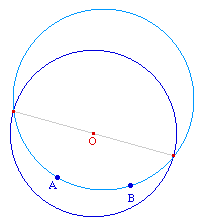
Soit C un cercle, A et B deux points à l'intérieur du cercle, tel que (AB) ne passe pas par le centre du cercle. Construire un cercle C' passant par A et B et sécant à C selon un de ses diamètres.
|
[Résultats
généraux] [Axe
radical] [Premières
applications de constructions]
[Problème
d'Appolonius] [Théorème
de Pascal][Retour
Géométrie 2D]
 |
Soit C un cercle, A et B deux points à l'intérieur du cercle, tel que (AB) ne passe pas par le centre du cercle. Construire un cercle C' passant par A et B et sécant à C selon un de ses diamètres.
|
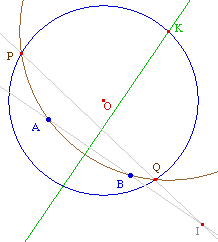 |
Soit un cercle intermédiaire passant par A et B (ci-contre centré en K sur le cercle C pour une transformation en macro). Ce cercle intermédiaire coupe C en P et Q.Les droite (AB) et (PQ) sont sécantes, car (AB) ne passe pas par O. Soit I l'intersection de ces deux droites.Alors, par construction, I a même puissance pour le cercle C que pour tout cercle passant par A et B. |
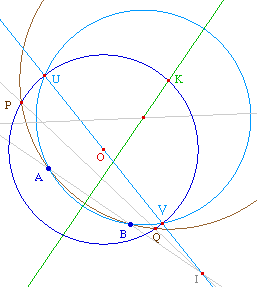 |
Remarque : Même si on n'utilise pas la notion de faisceau de cercles, on est en plein dedans.Et en particulier, si on note U et V l'intersection du cercle C et de la droite (OI), c'est le cas du cercle passant par A, B, U et V.En effet, A, B, U et V sont cocyclique.Le cercle passant par ces 4 points est donc solution.
|
[Résultats
généraux] [Axe
radical] [Premières
applications de constructions]
[Problème
d'Appolonius] [Théorème
de Pascal][Retour
Géométrie 2D]
|
|
|