Paraboles - Généralité
4 - Tangentes issues d'un point

[1 - Introduction] [2 - Intersection avec une droite] [3 - Tangente en un point] [5 - Constructions immédiates]
[Autres Propriétés] [Retour "Présentation Parabole"] [Retour "Coniques"]

 

On sait - page précédente - que la tangente en un point P d'une parabole de foyer F est la médiatrice de [FM] où M est la projection orthogonale de P sur la directrice.

 

Généralités

Soit T un point n'appartenant pas à une parabole. On cherche à construire les tangentes à la parabole issues de T.

Soit P un point de contact cherché. On sait que la tangente (TP) est médiatrice de F et de la projection M de P sur la directrice d. Donc TM = TF, ainsi les projections des points de contacts possibles sur la directrice sont aussi sur le cercle de centre T passant par F. Il y a donc au plus deux tangentes à la parabole issues d'un point.

Conditions d'existence de telles tangentes

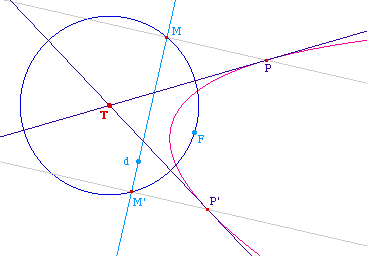
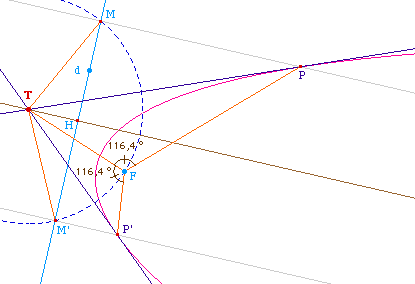
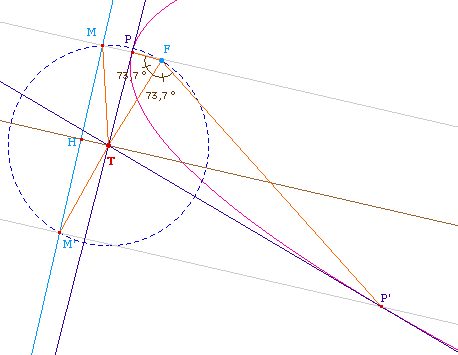
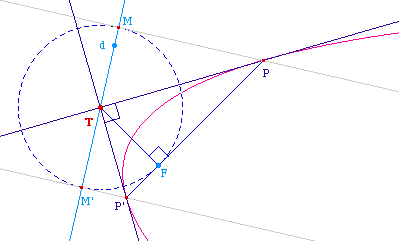
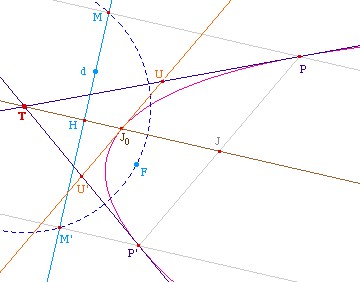
Les points M et M' existent si et seulement si le cercle de centre T passant par F coupe la directrice d, soit, en notant H la projection de T sur d si et seulement si TF > TH ce qui est équivalent à dire que T est extérieur à la parabole. D'où le résultat :

Par un point extérieur à une parabole il passe deux tangentes à cette parabole, données par la construction précédente.

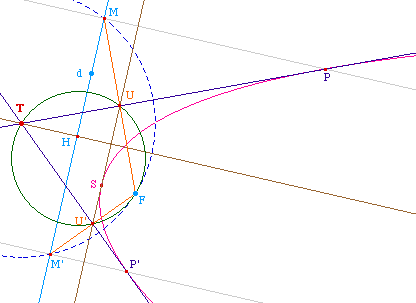
Remarque : En utilisant l'homothétie de centre F de rapport 1/2, on peut également construire les tangentes issues de T en remarquant qu'elles passent aussi à l'intersection du cercle de diamètre [TF] et de la tangente au sommet de la parabole.

La figure PBIssue1.fig ci-contre.

Macros associées

La figure précédente est transformable en macro, prise au sens d'une construction règle et compas, c'est à dire avec des objets finaux construits à partir des éléments définissant la parabole.

Charger la macro TPIssue.mac d'objets initiaux F, d et un point T extérieur à la parabole

On peut aussi utiliser une macro qui n'a comme abjets initiaux que l'objet conique parabole et un point extérieur. Cette macro a été construite à partir de la notion de polaire d'un point par rapport à une conique dans cette page de présentation projective sur les coniques par Michel Guillerault.

Charger la macro TgtExtCn.mac d'objets initiaux une parabole et un point extérieur.

 

Propriété angulaire des tangentes issues d'un point

 

De plus (TH) - la parallèle à l'axe passant par T - est axe de symétrie de la directrice et du cercle de centre T. Donc M et M' sont symétriques par rapport à cette droite. Comme le symétrique de P appartient à la droite (M'P') on peut dire que les angles géométrique en M et M' des triangles TMP et TM'P' sont égaux. Par symétrique de chacun d'eux par rapport à la tangente correspondante à la parabole, on peut dire que les angles géométriques TFP et TFP' sont égaux.

Ceci peut se résumer de deux façons (Premier théorème de Poncelet) :

Soit T un point extérieur à une parabole de foyer F, P et P' sont les points de contact de la parabole avec les tangentes issues de T. Alors :

1 - La droite (TF) est bissectrice intérieure de l'angle PFP'.

2 - Les segment [TP] et [TP'] des tangentes sont vus de F sous un même angle.

 

Cas où T est dans le même demi-plan que F par rapport à la directrice

 

Une première conséquence : la courbe orthoptique de la parabole

 

La courbe orthoptique d'une courbe C est l'ensemble des points d'où on voit C sous un angle droit, c'est-à-dire l'ensemble des points d'où il existe deux tangentes à C orthogonales entre elles.

Pour la parabole, on a vu que (TP) et (TP') sont les bissectrices intérieures des angles MTF et M'TF. Il en résulte que l'angle MTM' est le double de l'angle PTP'. Ce dernier est droit si et seulement si le premier est plat soit si et seulement si T appartient à la directrice.

La figure PBOrtho.fig ci-contre).

La courbe orthoptique d'une parabole est sa directrice

 

On notera également que la corde [PP'] passe par F et que F est le projeté orthogonal de T sur [PP'], puisque T étant sur la directrice TFP est rectangle en F. Cet argument est aussi une autre piste de preuve de ce résultat sur la courbe orhoptique, directement, sans l'argumentation angulaire précédente, en raisonnant sur le cercle circonscrit à MM'F et la position de son centre ...

Tangente et diamètre conjugué

Enfin, puisque H est milieu de [MM'], et que (TH) est parallèle à l'axe de la parabole, on peut remarquer que la droite (TH) est le diamètre conjugué de la direction de cordes (PP') :

Soit T un point extérieur à une parabole et P et P' les points de contact de cette parabole avec ses tangentes issues de T. Alors T appartient au diamètre conjugué de la direction (PP').

De plus l'intersection J0 de (TH) avec la médiatrice de [HF] est le point de la parabole donc cette médiatrice est tangente. Comme elle est sur (TH) c'est l'origine du diamètre conjugué comme déjà vu à cette illustration. Il en résulte que la médiatrice de [HF] est parallèle à (PP'). Il en résulte (Thalès) que J0 est le milieu de [UU'].
 

Remarque : On montrera, dans la partie "Autres Propriétés", que U et V sont aussi les milieu de [TP] et de [TP'] ce qui donnera alors la possibilité de construction d'une Cabri-parabole connaissant 2 tangentes et ses deux points de contact.

 

 

 [1 - Introduction] [2 - Intersection avec une droite] [3 - Tangente en un point] [5 - Constructions immédiates]
[Autres Propriétés] [Retour "Présentation Parabole"] [Retour "Coniques"]

 

  Menu général