La courbe orthoptique d'une courbe C est l'ensemble des points d'où on voit C sous un angle droit, c'est-à-dire l'ensemble des points d'où il existe deux tangentes à C orthogonales entre elles.

On se propose ici de l'étudier sur la base des propriétés les plus élémentaires des paraboles : la médiatrice de [FM] est la tangente en P à la parabole, si M est la projection de P sur la directrice.

La courbe orthoptique est contenue dans la directrice

Soit T un point extérieur à la parabole. On cherche à quelle condition les tangentes issues de T sont orthogonales. On conserve les mêmes notations qu'aux pages précédentes, en particulier U et U' sont les milieux de [FM] et [FM']. Le triangle PTP' est rectangle en T. On sait que FUT ey FU'T sont aussi droits puisque la tangente en un point P est la médiatrice du foyer et de la projection M de P sur la directrice.

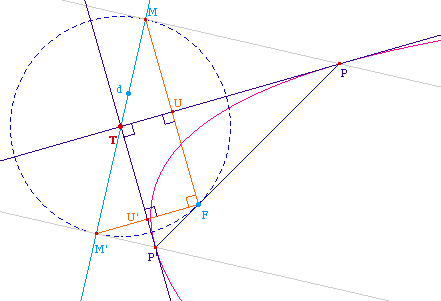
La directrice est contenue dans la courbe orthoptique

La réciproque est immédiate : si T appartient à la directrice, le triangle MFM' est droit car TM = TM' = TF.

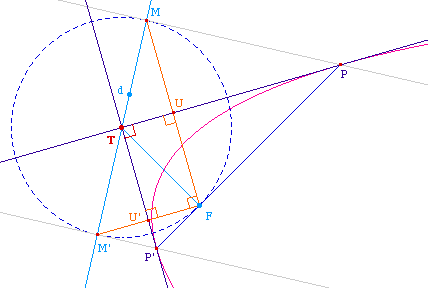
Cette fois-ci, le quadrilatère FUTU' a ses angles en U, F et U' droits, donc celui en T aussi.

[PP'] est une corde focale et (TF) lui est orthogonale

Les cercles de centre P et P' passant par F sont tangents à la directrice. T, milieu de [MM'] a même puissance par rapport à chaque cercle, il est donc sur l'axe radical. F aussi. Or, dans le triangle rectangle MFM', TM = TF, donc (TF) est une tangente à chacun des deux cercles, ce qui signifie que F est un point où les cercles sont tangents entre eux, et donc que F est sur la droite des centres (PP').

Ainsi, la corde [PP'] contient le foyer, et comme (TF) est l'axe radical des deux cercles, F est la projection orthogonale de T sur la corde.

Retour

Menu général