Autres propriétés des paraboles
1 - Cordes d'une parabole

 [2 - Second théorème de Poncelet] [3 - Tangentes et similitudes] [4 - Enveloppes]
[Premières propriétés des paraboles] [Retour "Présentation Parabole"] [Retour "Coniques"]

 

Nous nous proposons dans cette page d'observer simplement comment se généralise certaines propriétés sur les tangentes aux cordes d'une parabole. Des exercices de construction intéressants seront proposés sur la base de cette légère extension des résultats.

 

Résultat général

Soient A et B deux points de la parabole de foyer F et de directrice d. K désigne le projeté de F sur la directrice. Les cercles de centre A et B passant par F sont tangents à la directrice en M et N. Le milieu I de [AB] se projette en U sur la directrice et en V sur l'axe focal. Soit P l'intersection de l'axe focal et de la médiatrice de [AB]. On notera que KF est le paramètre de la parabole.

La directrice est la tangente commune aux deux cercles sécant (au moins) en F. Comme I est le milieu de [AB], U est le milieu de [MN], et donc UM = UN; ce qui signifie que U est sur l'axe radical des deux cercles car la puissance de U par rapport à chacun d'eux est respectivement UM2 et UN2 qui sont égaux. D'où le premier résultat :

(UF) est orthogonal à (AB)

Il en résulte que (IP) et (UF) sont parallèles et donc que les triangles IVP et UKF sont homothétiques (au sens large de l'image par une homothétie-translation). Comme par construction UK = IV, ils sont en translation et donc, on a :

VP = KF le paramètre de la parabole

PPCorde1.fig

Remarque : le premier résultat est une généralisation du fait que (TF) est orthogonal à (FP) si (TP) est tangente à la parabole en P et T son intersection avec la directrice. La seconde propriété est une généralisation du résultat relatif à la sous-normale.

 

Cordes focales

Ce sont les cordes qui passent par le foyer. On désigne toujours par U la projection orthogonale du milieu I de [AB].

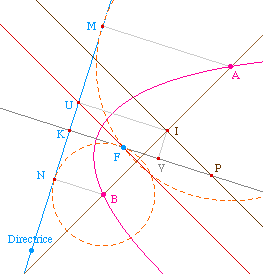
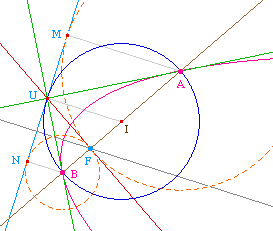
L'axe radical des deux cercles est toujours (UF) mais F etant maintenant un point de contact des deux cercles, le triangle UFA est rectangle en F, comme UMF : les deux ont même hypothénuse [AU], et même longueur d'un côté de l'angle droit (AF = AM), ils sont égaux, et donc symétriques par rapport à la droite (UA). Ainsi :

Les droites (UA) et (UB) sont les tangentes en A et B de la parabole.

Comme elles se coupent sur la directrice, on sait qu'elles sont orthogonales et donc que AUB est rectangle en U. Soit le résultat suivant :

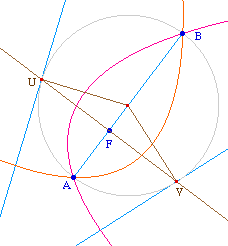
Le cercle de diamètre une corde focale [AB] est tangent à la directrice au point commun des tangentes à la parabole issues de ces deux points.

PPCorde2.fig

Exemple de construction

Or ce point de contact U est simplement l'intersection du cercle de diamètre [AB] avec la perpendiculaire à (AB) en F, puisque (UF) est l'axe radical des deux cercles, de centre A et B, passant par F. On peut donc facilement construire les paraboles de corde focale [AB] et de foyer F donnés :

PPCorde3.fig

ParaCfF.mac d'objets initiaux A, B et F sur [AB].

 

 [2 - Second théorème de Poncelet] [3 - Tangentes et similitudes] [4 - Enveloppes]
[Premières propriétés des paraboles] [Retour "Présentation Parabole"] [Retour "Coniques"]

 

Menu général