Ce théorème est relatif aux tangentes à une parabole issues d'un point dont les premières propriétés angulaires ont déjà été vues. Il nous sera utile pour le théorème relatif aux tangentes et aux similitudes

Remarque sur les bissectrices d'angles de vecteur

Soient (OA, OB) et (OA, OC) deux angles de vecteurs de même "origine" le vecteur OA. Soient alors (OM) et (ON) les bissectrices de ces angles, alors l'angle de droite (OM, ON) est égal à la moitié de l'angle de vecteur (OB, OC). (Il suffit d'écrire une relation de Chasles d'angle de droites)

Le second théorème de Poncelet

Reprenons l'illustration déjà étudiée lors des premières propriétés angulaires. M et M' désignent toujous les projections orthogonales es points de contact P et P' des tangentes issues de T. Ces tangentes ont leurs segments [TP] et [TP'] qui sont vus du foyer F sous le même angle. Désignons par [Tx) la demi-droite parallèle à l'axe, issue de T, dirigée vers l'intérieur de la parabole.

 

Illustration dans le cas où T et F sont de part et d'autre de la directrice

 

La droite (Tx) est médiatrice de [MM'] et la droite (TP) est médiatrice de [FM]. Elles sont donc, respectivement, bissectrices des angles de vecteurs (TM, TM') et (TM, TF). Donc d'après le rappel, elles forment un angle de droite égal à la moitié de l'angle de vecteur (TF, TM'), c'est à dire à l'angle (TF, TP'). On a donc ce premier résultat, en angles de droite : (Tx,TP) = - (TF, TP') La figure PPPonc01.fig ci-contre.

Illustration dans le cas où T est du même côté de la directrice que F

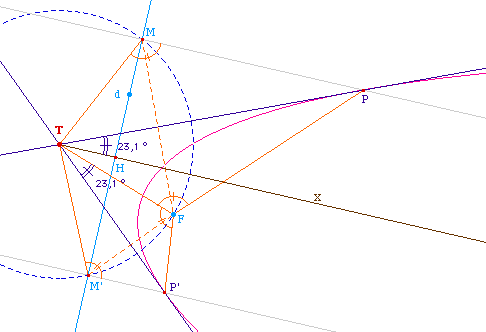
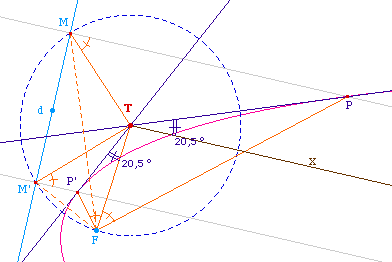
On peut préciser un peu plus : si on note, comme à la page sur les tangentes issues d'un point, U et U' les projection orthogonales de F sur (TP) et (TP'), on sait déjà que [TF] est le diamètre du cercle circonscrit au triangle TUU' et que (Tx) est la hauteur issue de T , car (UU') est la tangente au sommet, parallèle à la directrice.   Mais surtout, F et [Tx) étant intérieurs au secteur angulaire PTP', on peut dire que l'égalité d'angles de droite ci-dessus, est en fait une égalité d'angles de vecteurs. On a ainsi le second théorème de Poncelet : Les angles de vecteurs (TP, TP') et (Tx, TF) ont même bissectrice intérieure et les angles de vecteurs (TP,Tx) et (TP', TF) sont opposés.   Remarque : On notera que l'égalité d'angle est bien entendu indépendante de l'ordre des points de contact P et P' !!!

Menu général