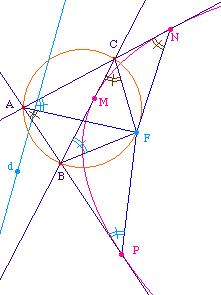
Nous reprenons la figure déjà utilisée pour la directrice comme droite de Steiner et nous la complétons avec les résultats angulaires du second théorème de Poncelet : par trois points d'une parabole on même les tangentes. Elles se coupent en A, B et C. Fixons les tangentes (AN) et (AP) et faisons varier la tangente (BC) par son point de contact M.

Premier point de vue
(avec la droite de Steiner)

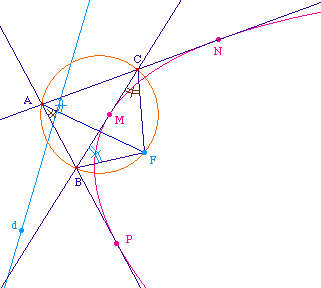
On sait que A, B, C et F sont cocycliques et donc en angles de droites, on a (BF, BC) = (AF, AC) et (CB, CF) = (AB, AF). D'où, si les tangentes (AN) et (AP) sont fixes, le triangle BFC conserve ses angles de droite constants, il reste donc directement semblable à lui-même quand M varie sur la parabole.

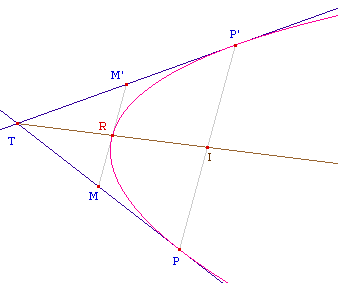
Second point de vue
(n'utilise pas la droite de Steiner)

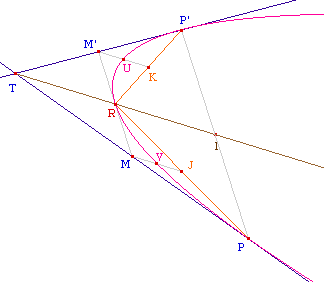
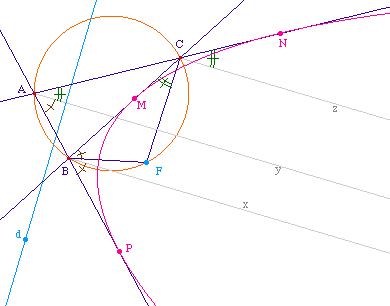
Le théorème de Poncelet permet de dire que les angles de droite (BP, Bx), (AP, Ay) et (BF, BC) sont égaux et qu'il en est de même pour les angles de droite (Ay, AN), (CB, Cz) et (Cz, CN). Ainsi, le triangle BFC ayant ses angles de droite constant, il reste directement semblable à lui même.

PPSimil1.fig

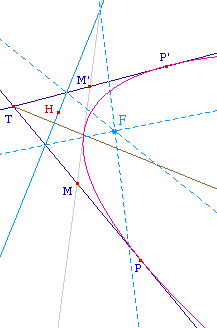
Remarque : Dans les deux illustrations ci-dessus, on pourrait penser que les égalités sont en angle de vecteur, mais ce n'est le cas que parce que B et C sont respectivement entre A et P, et A et N, c'est-à-dire M entre N et P.

Pour les cas particuliers de M en P ou M en N, le triangle BFC devient respectivement PFA et AFN. Ainsi, les trois triangles BFP, PFA et AFN sont directement semblables, et le rapport de similitude permet d'écrire les égalités :

^(*)

Puisque les angles PFA et AFN sont égaux (les segments de tangentes issues d'un point sont vus sous le même angle), F est le centre de la similitude directe qui transforme P en A et A en N ainsi que B en C. En particulier, on a aussi:

d'où on tire

On considère alors un point M de (Ax) et son image M' dans la similitude directe de centre F qui transforme P en P' (et Q en Q'). Pour cette dernière construction on peut :

Charger la macro SimSAA'M.mac d'objets initiaux S, A, A', et M : le centre de la similitude, un point A, son image A', et le point M dont on veut l'image. Résultats :

La figure PPSimil2.fig

Soient alors U et U' les symétriques de F par rapport à (Ax) et (Ax'). On considère la parabole de directrice d = (UU') et de foyer F. Par construction (Ax) et (Ay) sont deux tangentes à la parabole. F appartenant au cercle circonscrit de APP' et AQQ', la droite de Steiner de F relativement à ces deux triangles existe et c'est la droite (UU'). Donc la parabole est tangente aux droites particulières (PP') et (QQ'). Mais F appartenant aussi au cercle circonscrit de AMM' - par construction du centre de similitude qui envoie P en P' et M en M' - la droite de Steiner de F relativement au triangle AMM' existe et c'est toujours la directrice (UU'). Ainsi, le symétrique de F par rapport à (MM') appartient à la directrice, et donc (MM') est tangente à la parabole fixe définie par les points P, P', Q, Q'.

Nous pouvons revenir maintenant à la dernière figure de la page sur les tangentes issues d'un point et compléter un résultat partiel obtenu alors.

On considère une parabole définie par deux tangentes issues de T et leurs contacts P et P'. La similitude - de centre le foyer de la parabole - qui transforme P en T et T en P', transformera le milieu M de [TP] en le milieu M' de [TP']. D'après ce qui précède, la droite (MM') est aussi tangente à la parabole et le point de contact R est défini par la relation (*) ci-dessus : c'est donc le milieu de [MM'] puisque M est celui de [TP].

Par des arguments d'homothétie, il est clair que (MM') est paralèle à la corde (PP') et que R est le milieu de [TI] où I désigne le milieu de la corde.

Cette propriété donne en effet un procédé de construction d'un nombre quelconque de points de la parabole entre P et P'. En effet, R et P' étant à nouveau deux points de la parabole, on applique le même procédé : soit K le milieu de [RP'] et U le milieu de [M'K], pour les mêmes raisons, U est un point de la parabole. On sonstruit de même un cinquième point V, à partir de R et P, et on dispose ainsi de 5 points d'une parabole, ce qui permet une Cabri-construction.

PPSimil3.fig ci-contre

Remarque : Ce résultat est particulièrement intéressant, et peut être présenté trés simplement, mais de manière analytique, en lycée à partir de la classe de 1°S, sur la base d'une parabole d'équatin y = ax².

La macro Para2T2C.mac d'objets initiaux : le point d'intersection des tangentes, une première tangente et son contact, la seconde tangente et son contact.

Dans ce cas, retrouver la directrice et le foyer est élémentaire puisque la droite (TI), diamètre conjugué de la corde (PP'), est parallèle à l'axe de la parabole : on connait donc la direction de la directrice. De plus elle passe par l'orthocentre du triangle TMM' : on connait donc la directrice. L'intersection des images de la directrice dans deux symétries orthogonales par rapport à deux des trois tangentes, donne alors le foyer.

PPSimil4.fig ci-contre

La macro Pfd2T2C.mac d'objets initiaux les mêmes que ci-dessus qui renvoie en plus la directrice et le foyer.