Nous nous proposons dans cette page de montrer un résultat déjà vu par des arguments de similitude, avec un simple calcul algébrique accessible dès la classe de 1°S :

Soient deux droites, tangentes à une parabole en P et P'. On note T leur point d'intersection, et I le milieu de [PP']. Alors le milieu R de [TI] est un point de la parabole en lequel la tangente est parallèle à la corde [PP'].

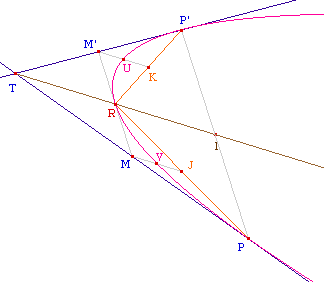
Mise en place des notations

Soient A et B deux points d'une parabole, T le point d'intersection des tangentes en A et B. On se place dans un repère pour lequel la parabole est d'équation y = ax².

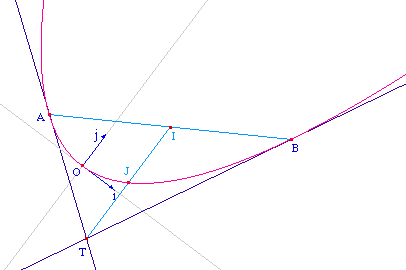
Lancer la figure Cabri ci-dessus (fichier "PPAnaly1.fig").

I est le milieu de [AB] et J celui de [TI]. Si on note A(x_A, y_A) et B(x_B, y_B), on a :

Coordonnées du point T

Le milieu I de [AB] a pour coordonnées ((x_A+x_B)/2, (y_A+y_B)/2).

Equation de la tangente en A : y - y_A = 2ax_A(x - x_A)

Equation de la tangente en B : y - y_B = 2ax_B(x - x_B)

L'intersection T des deux tangentes a donc pour abscisse x_T tel que :

2ax_A(x_T - x_A) + y _A = 2ax_B(x_T - x_B) + y_B.

Ce qui aboutit à x_T = (x_A + x_B)/2 soit x_T = x_I

Remarque : Ainsi (TI) est paralléle à l'axe de la parabole, on retrouve le rayon conjugué à la direction de la corde.

Ce qui donne y_T = ax_Ax_B.

 

Coordonnées du point J, milieu de [IT]

Son abscisse est donc celle, commune, de I et de T : x_J = (x_A+x_B)/2

Son ordonnées est [ (y_A+y_B)/2 + ax_Ax_B]/2 soit (y_A+y_B + 2ax_Ax_B]/4

Et donc y_J = a[(x_A+x_B)/2]². Soit J appartient à la parabole.

 

Nombre dérivé en J

y'_J = 2a[(x_A+x_B)/2] = a(x_A+x_B).

Or ce nombre n'est rien d'autre que la pente de la droite (AB) :

(y_A - y_B)/(x_A - x_B) = a(x_A+x_B)

La tangente en J est parallèle à (AB).

 

Itération successives

Puisque l'on trouve un nouveau point J et sa tangente, sur l'arc de parabole [AB], on peut réitérer l'argument avec les points J et A ou J et B et trouver deux autres points de la parabole et leurs tangentes.

Retour

Menu général