[1
- Cordes d'une parabole]
[2
- Second théorème de Poncelet] [3
- Tangentes et similitudes]
[Premières
propriétés des paraboles] [Retour
"Présentation Parabole"]
[Retour
"Coniques"]

|
|
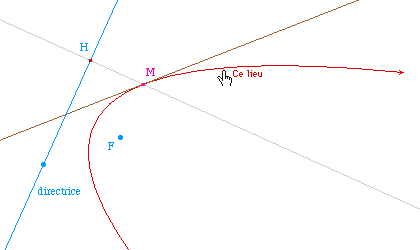
On en déduit la génération tangentielle suivante :L'enveloppe d'une droite pour laquelle le symétrique H d'un point fixe F par rapport à cette droite décrit une droite d est une parabole de foyer F et de directrice d. |
|
|
Par ailleurs, la projection orthogonale de F sur cette médiatrice décrit l'homothétique de la directrice dans l'homothétie de centre F de rapport 1/2, dont on sait que c'est la tangnete au sommet de la paraboleOn en déduit une autre écriture de cette même génération tangentielle:Soit F un point fixe. L'enveloppe de la droite perpendiculaire en H au segment [HF], quanf H décrit une droite d, est une parabole de foyer F et de tangente au sommet la droite d. |
L'enveloppe des droites (MM') qui partagent sur deux droites non paralléles (PQ) et (P'Q') les segments [PQ] et [P'Q'] dans le même rapport est une parabole tangente aux deux droites (PQ) et (P'Q').
