[Retour Présentation]
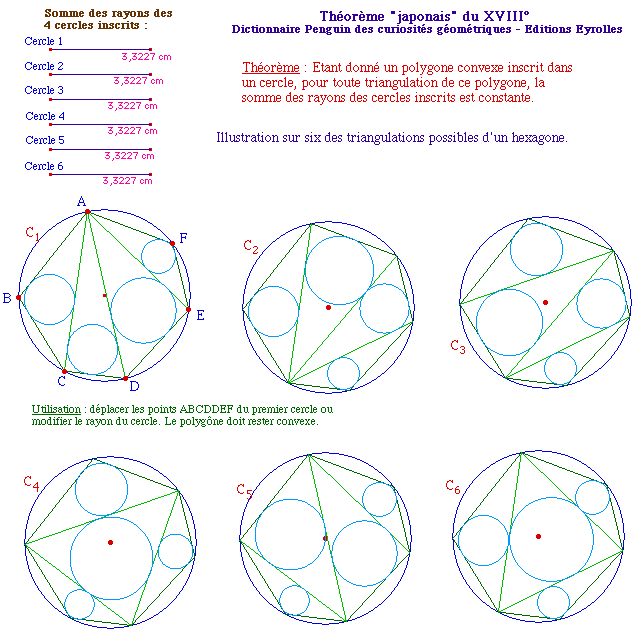
[1 - Résultat historique]
[2 - Le théorème de
Ptolémée]
[3 - Un premier problème de
distance] [4 - Application : Le
problème de Fermat]
[5 - Application : La loi de la
réfraction]
[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]

- On commence par le montrer pour un quadrilatère.
- Puis on continue par récurrence sur le nombre de côtés du polygone convexe, en étant attentif à montrer que l'on peut effectivement utiliser l'hérédité dans la preuve par récurrence.
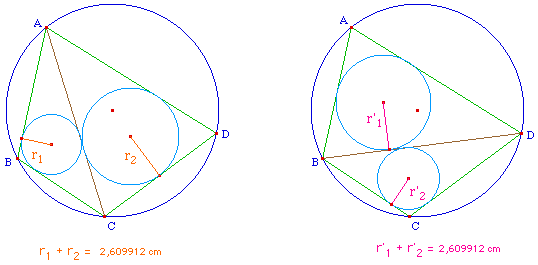
En notant a, b, c les côtés d'un triangle, R et r les rayons des cercles circonscrit et inscrit on sait que 2Rr = abc/(a+b+c) qui s'obtient par exemple à partir de abc/4R = S = pr (avec p le demi périmètre).
Sur la figure ci-dessus, on note a, b, c, d les longueurs AB, BC, CD, DA, puis m = AC et n = BD.
On notera S1, S2 les aires de ABC et ACD, S'1 et S'2 les aires de ABD et BCD.
ABCD inscrit signifie que les quatres triangles en jeu ont même cercle circonscrit de rayon R.
Le fait que ABCD soit convexe entraine que S1 + S2 = S'1 + S'2 = S l'aire de ABCD, ce qui se traduit par :
(ab + cd) m = (ad + bc) n = S, en multipliant les aires par le rayon R commun aux 4 triangles.
Le théorème de Ptolémée (inscrit + convexe) permet d'écrire ac + bd = mn.
On part de
et
On montre alors, à l'aide des relations ci-dessus, que le rapport des deux (r1+r2) / (r'1+r'2) est égal à 1.
- Vrai pour n = 4 (étape 1)
- Pour n supérieur, dans toute triangulation du polygone, il existe un triangle formé de trois points consécutifs Ai-1AiAi+1, sinon on n'a pas une triangulation (on se ramène au cas n=4).
- Considérons un triangulation. On peut supposer, à une renumérotation près, qu'elle contient le triangle A1A2A3.
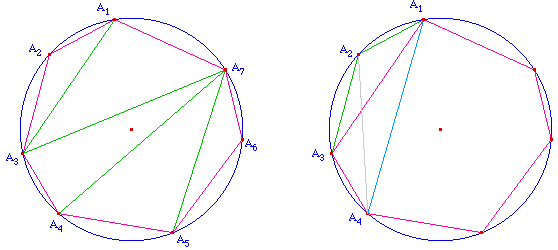
- On applique alors l'hypothèse de récurrence sur A1A3A4...An, le cas n = 4 sur A1A2A3A4. Il en résulte que le résultat est vrai pour la triangulation contenant A1A2A4 et A2A3A4, donc par hypothèse de récurrence pour toute triangulation contenant A2A3A4.
- On atteint ainsi toutes les triangulations possibles
Pour tous réels a et b, on a :
2sin a sin b sin (a+b) = [sin a + sin b + sin (a+b)].[-1 + cos a + cos b - cos (a+b)]
Se vérifie par exemple avec un logiciel de calcul formel.
Etant donné deux points A et B d'un cercle de centre O de rayon R, et a la mesure de AOB entre 0 et Pi, on a AB = R. sin (a/2).
Immédiat.
En reprenant les notations précédentes, on a r = a.b.c / 2R(a + b + c).
Déjà vu ci-dessus
|
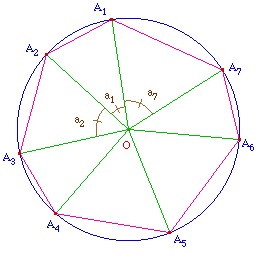
On dispose de n points A1, ... An dans cet ordre, sur un cercle de centre O et de rayon R. On considère un pavage P du polygone (A1, ..., An) formé de triangles AiAjAk. On définit ainsi n-2 triangles. On notera ai l'angle géométrique en O du triangle AiOAi+1 et an celui de AnOA1.On remarque que an = 2Pi - (a1 + ... + an-1). On notera bi = ai / 2.On se propose de trouver une expression de la somme Sr des rayons des cercles inscrits des triangles de P. Et montrer qu'elle est indépendante du pavage P.
Théorème
:
|
[Retour Présentation]
[1 - Résultat historique]
[[2 - Le théorème de
Ptolémée]
[3 - Un premier problème de
distance] [4 - Application : Le
problème de Fermat]
[5 - Application : La loi de la
réfraction]
[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]