Cocyclicité et
distance
4 - Application de
Ptolémée : le problème de Fermat
[Retour Présentation]
[1 - Résultat historique]
[2 - Le théorème de
Ptolémée]
[3 - Un premier problème de
distance] [5 - Application : La
loi de la réfraction]
[6 - Application : Cercles inscrits et
partitions d'un polygone inscrit]
[Retour
Angle/Cocyclicité] [Autres
exercices utilisant la cocyclicité] [Retour
Géométrie 2D]
Le problème de Fermat
Soient un triangle ABC et un point M quelconque de
son plan.
Minimiser la somme MA + MB + MC.
Résolution
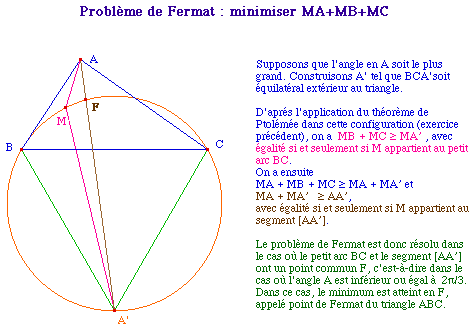
L'idée est de minimiser
d'abord MB + MC pour se ramener ensuite à une
inégalité triangulaire. Pour cela, supposons par
exemple que l'angle en A soit le plus
grand angle et construisons
extérieurement au triangle ABC un triangle
équilatéral BCA' et son cercle circonscrit. Nous
allons utiliser le résultat
précédent sur le triangle
équilatéral.
 Fermat1.fig
Fermat1.fig
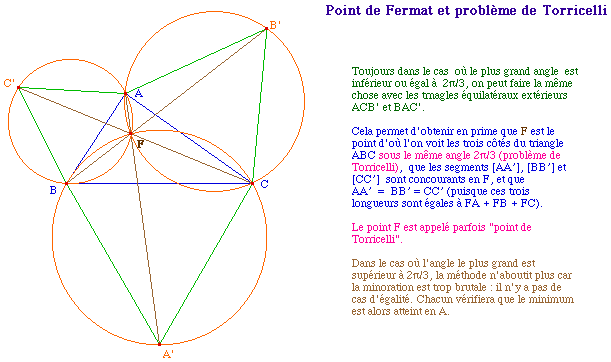
 Fermat2.fig
Fermat2.fig
[Retour Présentation]
[1 - Résultat historique]
[2 - Le théorème de
Ptolémée]
[3 - Un premier problème de
distance] [5 - Application : La
loi de la réfraction]
[6 - Application : Cercles inscrits et
partitions d'un polygone inscrit]
[Retour
Angle/Cocyclicité] [Autres
exercices utilisant la cocyclicité] [Retour
Géométrie 2D]
 Menu
général
Menu
général

