Extrait de l'Almageste

Voici pour commencer le résultat tel qu'il fut énoncé et démontré par Ptolémée dans son traité l'Almageste :

 

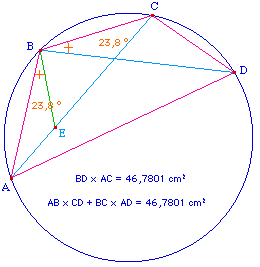
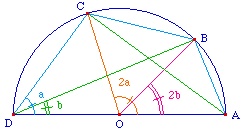
« Soit un quadrilatère quelconque inscrit dans le cercle ABCD ; soient menées les diagonales AC, BD : il s'agit de prouver que AC x BD = AB x CD + BC x AD Soit fait l'angle ABE égal à l'angle DBC ; si nous ajoutons à chacun l'angle commun EBD, l'angle ABD est égal à l'angle EBC. Mais BDA = BCE ; car ces deux angles sont inscrits et appuyés sur le même arc ; donc le triangle ABD est équiangle au triangle BCE. On a donc la proportion BC : CE = BD : DA. Et par conséquent BC x DA = CE x BD. Maintenant puisque l'angle ABE est égal à l'angle DBC, et que l'angle BAE est égal à l'angle BDC, le triangle ABE est équiangle au triangle BCD. On a donc la proportion BD : DC = BA : AE, et donc BA x DC = BD x AE. Or il a été prouvé que BC x AD = BD x CE ; par conséquent BD x AC = BAxDC + BCxAD. Ce qu'il fallait montrer. » Almag1.fig

Voir une page de l'Almageste (dans abraCAdaBRI 110 Ko) - Lien sur d'autres extraits de l'Almageste

 

On notera les faiblesses de ce texte : le quadrilatère est implicitement supposé convexe et la démonstration dépend fortement de la position du point E. De plus, il ne s'agit que d'une condition nécessaire de cocyclicité. Ptolémée n'a en fait pas besoin de la réciproque : son but est seulement d'obtenir des relations équivalentes à nos modernes formules de trigonométrie et donc il travaille toujours à partir de points situés au départ sur un même cercle.

Utilisation en trigonométrie

Voici par exemple comment on peut (en langage moderne) prouver la relation sin(a - b) = sin a cos b - sin b cos a pour deux angles a et b tels a soit compris en b (positif) et Pi/2.

 

Almag2.fig

Considérons un quadrilatère ABCD inscrit dans un demi cercle de diamètre AD et de centre O, de sorte que AD = 1, Les triangles ABD et ACD étant rectangles, on a AB = sin b, AC = sin a, mais aussi BD = cos b et CD = cos a. Dans BCD la relation des sinus (a/sin A = 2R) donne BC = sin (a-b), toujours car AD = 1. Le théorème de Ptolémée affirme que AC x BD = AB x CD + BC x AD, soit encore, puisque AD = 1 : sin(a - b) = BC = AC x BD - AB x CD, d'où la relation sin(a - b) = sin a cos b - sin b cos a.

Menu général