Cette page sert essentiellement de lien entre le théorème de Ptolémée et son application au "problème de Fermat" : on considèrera le résultat comme une application directe.

Ce problème est en général traité dans les manuels scolaires (PS ou TS) soit par les rotations, les complexes ou encore la géométrie analytique.

PtoEqui.fig

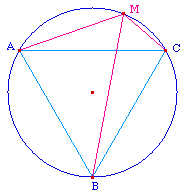
Soient ABC un triangle équilatéral et M un point de son cercle circonscrit. Montrer que l'une des distances MA, MB et MC est égale à la somme des deux autres. Supposons par exemple que M soit sur l'arc AC qui ne contient pas B. Le quadrilatère MABC est convexe et inscrit dans un cercle, donc d'après le théorème de Ptolémée, on a : MB.AC = MA.BC + MC.AB. Le triangle ABC est équilatéral ; en simplifiant par AC = BC = AB, on obtient MB = MA + MC. De façon analogue, on a MC = MB + MA sur le petit arc AB et MA = MB + MC sur le petit arc BC.

Remarquons que le théorème de Ptolémée prouve davantage : pour tout point M du plan n'appartenant pas au petit arc AC, on a l'inégalité stricte MB < MA + MC.

Cette exercice peut sembler anodin, toutefois il suggère une solution simple et naturelle au problème de Fermat.

Remarque : on consultera par exemple la première partie du sujet de CAPES interne 92 (seconde épreuve) pour trois autres preuves de ce résultat.

Menu général