Le théorème

Etant donnés quatre points A, B, C et D du plan, on a toujours l'inégalité  

et l'égalité a lieu si et seulement si A, B, C et D sont cocycliques ou alignés, dans cet ordre.

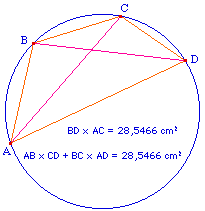En particulier : Dans un quadrilatère convexe inscrit dans un cercle est tel que le produit des diagonales est égal à la somme des produits des côtés opposés.

Si deux points (ou davantage) sont confondus, le résultat se vérifie immédiatement ; on peut donc supposer que les quatre points sont distincts. Travaillons dans le plan complexe et notons a, b, c, d les affixes respectives des points A, B, C, D. On a alors :

L'égalité dans l'inégalité triangulaire a lieu si et seulement si est un réel positif. On peut dire de façon équivalente que le birapport est réel négatif ou encore, en passant aux arguments, que .

C'est bien la condition pour que A, B, C et D soient cocycliques ou alignés, dans cet ordre.

 

Menu général