Cocyclicité et distance
5 - Application de Ptolémée : la loi de la réfraction

[Retour Présentation] [1 - Résultat historique] [2 - Le théorème de Ptolémée]
[3 - Un premier problème de distance] [4 - Application : Le problème de Fermat]
[6 - Application : Cercles inscrits et partitions d'un polygone inscrit]

[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]

 

La loi de Snell

Le problème de la réfraction de la lumière, lorsque celle-ci passe d'un milieu où elle se déplace à la vitesse v1 à un milieu où elle se déplace à la vitesse différente v2 peut se formuler géométriquement de la façon suivante :

Deux point A et B sont situés de part et d'autre d'une droite d. Pour quel point M de d le temps de parcours est-il minimum ?

Une façon de repérer le point M sur la droite d est d'introduire les angles d'incidence i et de réfraction r. Vers 1625, le Hollandais Snell a découvert expérimentalement la loi de la réfraction, appelée aussi loi de Snell : le minimum est atteint au point M de d tel que .

Nous allons démontrer cette loi grâce au théorème de Ptolémée.

 

Preuve avec le théorème de Ptolémée

 

Soit donc M le point défini par la loi de Snell (nous laissons le lecteur se convaincre par lui même que M existe et est unique) et soit N un point quelconque de la droite d. Le cercle passant par A, M et B recoupe la normale à d en C.

 

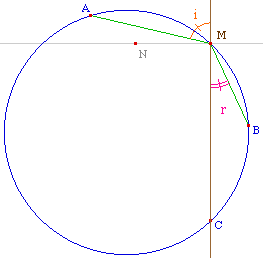
Refract1.fig

D'après le théorème de Ptolémée, on a 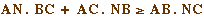, avec égalité si et seulement si A, N, B et C sont cocycliques dans cet ordre. Compte tenu du fait que N est sur d, l'égalité a lieu si et seulement si N = M.

On a ensuite 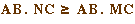avec égalité si et seulement si N = M , car M est le projeté orthogonal de C sur d. Enfin, A, M, B et C étant cocycliques dans cet ordre, on a l'égalité AB.MC = AM.BC + AC.MB. On obtient donc, pour tout point N de d, l'inégalité

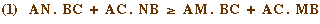
avec égalité si et seulement si N = M.

Un peu de trigonométrie permet d'obtenir les égalités

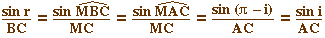
d'où BC.v1 = AC.v2. Les distances BC et AC étant ainsi inversement proportionnelles aux vitesses v1 et v2 , l'inégalité (1) équivaut à

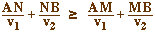
avec toujours égalité si et seulement si N = M, ce qui démontre bien que le minimum est atteint en M et en lui seul.

Bien sûr, cette preuve n'est possible que si on connaît d'avance le résultat. Snell l'a découvert expérimentalement ; on peut le découvrir aussi grâce au calcul différentiel : c'est ce qui est fait dans les manuels de Première en général. Il est de toute façon très formateur de mettre en oeuvre et de comparer diverses méthodes.

 

 

[Retour Présentation] [1 - Résultat historique] [[2 - Le théorème de Ptolémée]
[3 - Un premier problème de distance] [4 - Application : Le problème de Fermat]
[6 - Application : Cercles inscrits et partitions d'un polygone inscrit]

[Retour Angle/Cocyclicité] [Autres exercices utilisant la cocyclicité] [Retour Géométrie 2D]

 

 

 

Menu général