Visualisation du faisceau des orbites

 d'un système linéaire à coefficients constants (ordre 1 dimension 2)

Préambule

Les équations différentielles vont occuper une place importante dans les nouveaux programmes de PS et de TS, avec une approche qualitative fondée sur l'utilisation des ordinateurs et des logiciels de calcul formel (ou de géométrie !). Les TPE (Travaux personnels encadrés) seront un cadre idéal pour faire expérimenter les élèves sur ce thème.

Extrait des projets de programme (au 02/00) :

"Equation différentielle linéaire d'ordre deux à coefficients constants. Représentation des solutions de l'équation linéaire du second ordre dans l'espace des phases."

Comme une équation à coefficients constants d'ordre 2 en dimension 1 équivaut à un système à coefficients constants d'ordre 1 en dimension 2, et comme la représentation dans l'espace des phases n'est autre que le tracé des orbites, ce dossier d'abraCAdaBRI offre par avance aux professeurs de TS tout ce qu'ils auront à expérimenter et visualiser avec leurs élèves. Le dossier offre aussi aux enseignants le substrat d'algèbre linéaire qui leur permettra de classifier et d'organiser (sans le dire !) ce que les élèves découvriront empiriquement.

Signalons également que depuis 1998, il y a, à l'agrégation interne, une leçon d'oral qui s'intitule "Systèmes différentiels linéaires à coefficients réels constants en dimension 2. Allure des courbes intégrales." Ce dossier d'abraCAdaBRI devrait permettre aux candidats d'acquérir toutes les images mentales nécessaires pour pouvoir ensuite présenter une leçon cohérente, vivante et rigoureuse.

Objectif de cette page et principe théorique

On se propose d'observer l'allure générale des orbites du système . Pour cela, nous allons utiliser deux figures.

La première  SystLin1.fig (22 Ko), dans l'esprit de la visualisation avec la trace avec Cabri, construit le vecteur unitaire directeur de la tangente à l'orbite passant par le point courant. La modification des paramètres permet d'observer tous les cas possibles dans l'étude du système. Toutefois, pour chaque situation il convient de balayer à nouveau le plan avec le vecteur pour faire apparaître l'allure des orbites. Cette figure peut être intéressante à utiliser quand on veut induire une démarche de conjecture : l'écran est d'abord vide, le champ de vecteur est construit par l'utilisateur.

Dans une seconde figure, SystLin2.fig (85 Ko) nous construisons le champ de vecteur en plusieurs points du plan, plus précisément sur une partie de la grille des entiers et demi-entiers. Sur cette figure, le champ de vecteur est donc modifié directement en modifiant les paramètres du système. Cette figure est plus appropriée si on se propose simplement d'illustrer - de manière dynamique - les différents cas rencontrés, éventuellement aprés une étude théorique. Didactiquement, elle présente aussi l'intéret de pouvoir placer un point sur les directions propres ce qui permet de vérifier - conjecturer - si la direction propre fait partie du faisceau des orbites au pas : nous y reviendrons sur les exemples.

Principe de base

On considère la matrice du système A = . La méthode générale, issue de l'algèbre linéaire consiste - le plan étant rapporté à priori à une base canonique - à déterminer une nouvelle base dans laquelle la matrice du système aura une écriture plus simple. On étudie alors le système dans cette nouvelle base, d'où une discussion selon l'existence des valeurs propres et leurs valeurs.

 

Quatre illustrations avec les deux figures (parmi les 14 cas possibles)

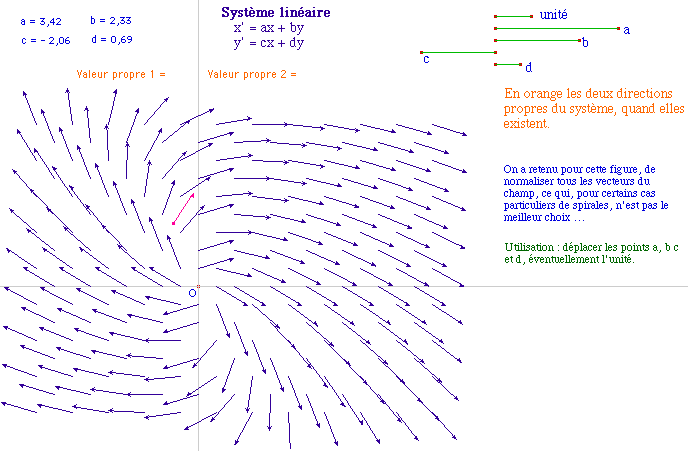
Les droites oranges sont les directions propres

Deux valeurs propres réelles distinctes, non nulles, de signe contraire

 

Même cas, avec le champ de vecteur en les points d'une grille

Deux valeurs propres réelles distinctes dont une nulle

Deux valeurs propres complexes conjuguées, cas où la partie réelle est négative.

 

Deux valeurs propres complexes conjuguées, cas où la partie réelle est positive

.

 

Les différents cas possibles

Le tableau suivant renvoie sur 18 pages différentes. Les 4 pages de la colonne de gauche contiennent les résultats théoriques, et les illustrations des différents sous-cas en vignette. Les pages des autres colonnes contiennent des illustrations dans les deux figures, en taille normale. Ces pages contiennent éventuellement quelques commentaires supplémentaires sur le comportement limite du champ de vecteur, par exemple sur les droites portées par les directions propres.

On peut aussi préférer un résumé graphique en une seule page soit avec les traces, soit avec la grille.

Si les pages suivantes ont été faites pour être vues ;-) il est certainement plus intéressant d'expérimenter soi-même soit en chargeant les deux figures d'illustration SystLin1.fig (22 Ko) pour la trace et SystLin2.fig (85 Ko) pour le champ sur une grille, soit en manipulant directement ces figures dans le navigateur en CabriJava, au choix avec la trace, ou avec la grille.

Merci à DominiqueTournès de m'avoir largement ouvert ses compilations et résumés de cours ... d'avoir passé du temps à me les commenter ;-) et d'avoir consacré autant de temps à vérifier les pages d'abraCAdaBRI. Ce dossier est en définitive la "Cabri - mise en ligne" de ses fiches.

Menu général