La solution générale du système est
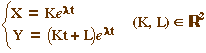
A admet une valeur propre double, mais n'est pas diagonalisable. Il existe donc une base dans laquelle la matrice du système est
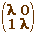
La solution générale du système est
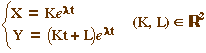
Les illustrations suivantes ont été réalisées en choisissant les coefficients pour que la matrice réduite le soit dans la base canonique. Ainsi, la direction propre est l'un des deux axes. Ci dessous, c'est clairement l'axe vertical pour les illustrations avec la trace par exemple.
Valeur propre négative
Valeur propre nulle
Valeur propre positive
|
|
||||
|
(homothétie) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Charger les figures utilisées
![]() SystLin1.fig
(22 Ko) pour la trace et
SystLin1.fig
(22 Ko) pour la trace et
![]() SystLin2.fig
(85 Ko) pour le champ sur une grille.
SystLin2.fig
(85 Ko) pour le champ sur une grille.
Manipulant directement ces figures dans le navigateur en CabriJava, avec la trace, ou avec la grille.
[Retour Système] [Retour EDO] [Retour "Courbes et équations"]