Système linéaire à coefficients constants (ordre 1 dimension 2)

Cas où le système a deux valeurs propres distinctes : 0 et une positives

Rappel du résultat

A admet deux valeurs propres réelles distinctes p > m. Il existe donc une base dans laquelle la matrice du système est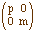

Dans cette base la solution générale du système est

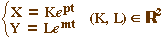
Ici nous sommes dans le cas où m vaut 0.

 

Illustrations

 

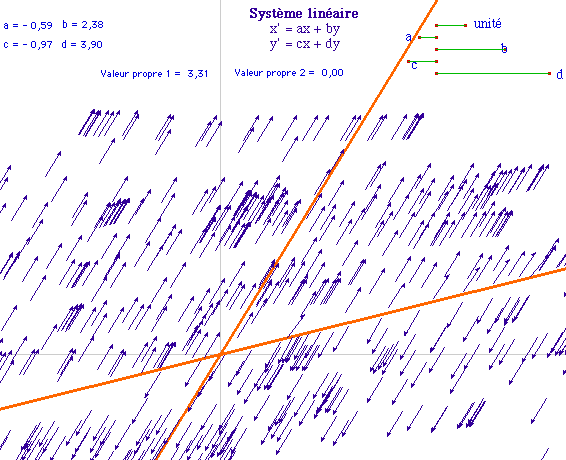
La direction propre associée à la valeur propre nulle n'est pas orbite.
Chaque point de cette droite est une orbite à lui tout seul. On notera qu'il est "répulsif" dans la direction de l'autre direction propre.

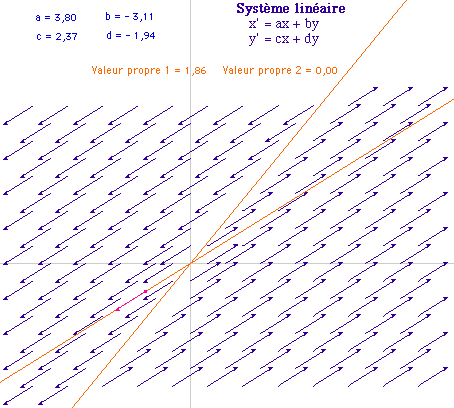
Ci dessus, on a placé le vecteur libre sur la direction propre associée à la valeur propre positive. On peut aussi le placer sur l'autre direction propre (par "redéfinir un point"). Alors le vecteur est réduit à un point : sur cette direction, les orbites se réduisent à des points isolés (comme vu ci-dessus).
On peut aussi plus simplement observer le changement de comportement du vecteur lors du franchissement de cette direction propre.

 

Navigation dans les différents cas du système

Pages des critères généraux	Les cas particuliers de ce critère général
A = aId (homothétie)	a est négatif	a est nul	a est positif
Deux valeurs propres réelles distinctes	Les deux négatives	Une négative l'autre nulle	De signes contraires	Une positive l'autre nulle	Les deux positives
Une valeur propre double, la matrice n'étant pas diagonalisable	La valeur propre est négative	La valeur propre est nulle	La valeur propre est négative
Deux valeurs propres complexes conjuguées	La partie réelle est négative	La partie réelle est nulle	La partie réelle est positive

Charger les figures utilisées SystLin1.fig (22 Ko) pour la trace et SystLin2.fig (85 Ko) pour le champ sur une grille.

Manipulant directement ces figures dans le navigateur en CabriJava, avec la trace, ou avec la grille.

Menu général