|
|
|
|
 |
 |
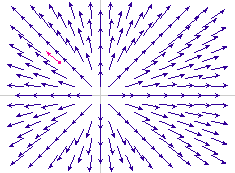 |
Les illustrations sont des liens. Les titres renvoient sur les solutions théoriques.
Valeur propre négative
Valeur propre nulle
Valeur propre positive
|
|
|
|
 |
 |
 |
|
|
|
 |
 |
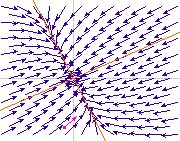
Valeur propre négative
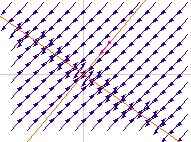
Valeur propre nulle
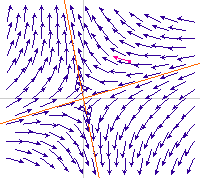
Valeur propre positive
|
|
|
|
 |
 |
 |
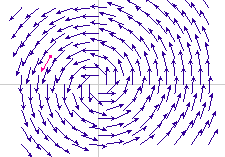
On peut choisir de charger les deux figures d'illustration
![]() SystLin1.fig
(22 Ko) pour la trace et
SystLin1.fig
(22 Ko) pour la trace et
![]() SystLin2.fig
(85 Ko) pour le champ sur une grille. On
peut aussi manipuler directement ces figures dans le navigateur
en CabriJava, soit avec la
trace, soit avec la
grille.
SystLin2.fig
(85 Ko) pour le champ sur une grille. On
peut aussi manipuler directement ces figures dans le navigateur
en CabriJava, soit avec la
trace, soit avec la
grille.