2. Applications à l'hyperbole équilatère | 3. Coniques harmoniquement inscrites et circonscrites
Plus de détails sur les pôles et polaires (propriétés, etc.)
En prenant PQR comme repère, et en exprimant les coordonnées homogènes de la conique et des polaires de trois points P', Q', R', Géry Huvent montre alors le :
2TRAuto1.fig - Voir la figure en
CabriJava
En fait la preuve précédente repose sur le fait que deux déterminants sont nuls en même temps. En réalité, en constatant que ces deux déterminants sont égaux simultanément, on aboutit au résultat suivant :
Soient PQR et P'Q'R' deux triangles. Alors les conditions suivantes sont équivalentes :
a) Il existe une conique C telle que les deux triangles soient autopolaires par rapport à C.
b) Il existe une conique C' qui passe par les six sommets de ces deux triangles.
Appel à Cabri construction : il serait intéressant, étant donnés un triangle PQR un point P' et une droite p' ne passant pas par P', de construire une conique pour laquelle PQR soit autopolaire, et p' la polaire de P. Cette conique devrait avoir un degré de liberté (par exemple passant par un point). Alors en choisissant ce point Q' sur la polaire p' de P', on devrait pouvoir illustrer cette généralisation de manière intéressante avec Cabri.
Les six côtés de deux triangles autopolaires par rapport à une conique sont tangents à une autre conique. Et plus généralement on a aussi :
Soient PQR et P'Q'R' deux triangles. Alors les conditions suivantes sont équivalentes :
a) Il existe une conique C telle que les deux triangles soient autopolaires par rapport à C.
b) Il existe une conique C' qui est tangente aux six côtés de ces deux triangles.
2TRAuto2.fig - Voir la figure en
CabriJava
On peut déduire aussi de ces deux théorèmes une autre propriété caractéristique illustrée ci-dessous. Pour cela, appellons conique inscrite à un triangle, une conique tangente à ces côtés, et circonscrite une conique passant par ses sommets.
La figure suivante est construite en 3 étapes - pour être manipulable en CabriJava. Sont illustrées ci-dessous la première (construction initiale), la deuxième (construction intermédiaire). La troisième (Cabri-vérification du théorème) n'est pas illustrée ici.
2TRAuto3.fig - Voir la figure en
CabriJava
Pour ce paragraphe - et uniquement lui - on utilise le résumé sur les points cycliques.
 |
Soit ABC un triangle et P une parabole, de foyer F inscrite dans ce triangle (ou encore ABC circonscrit à P). Le triangle FIJ est circonscrit à la parabole car la droite des points cycliques (IJ) est la droite de l'infini, dont on sait qu'elle est tangente à la parabole P et les droites (FI) et (FJ° sont les tangentes à la parabole issues de F. Il en résulte que les six points A, B, C, F, I et J sont alors sur une même conique qui, puisqu'elle passe par I et J, est un cercle affine. On vient donc de retrouver cette propriété euclidienne bien connue : Soit ABC un triangle circonscrit à une parabole. Alors le cercle circonscrit à ABC passe par le poyer de cette parabole. Nous avons vu une preuve plus "classique" à cette page. On peut aussi retrouver une illustration dynamique en CabriJava à cette autre page. |
Le théorème de Poncelet, très général, va nous permettre de retrouver plusieurs résultats. Il suffit pour cela de choisir des triangles autopolaires significatifs. Commençons par quelques définitions :
 |
Soit ABC un triangle et M distinct des sommets. Les droites (AM), (BM) et (CM) sont dites céviennes (à cause du théorème de Céva). Elles coupent - en général - les côtés opposés du triangles en trois points PQR. Le triangle PQR est dit triangle cévien de M par rapport au triangle ABC, et son cercle circonscrit est dit cercle cévien de M par rapport au triangle ABC. |
 |
Si les points A, B, C et M sont sur une même conique, on voit que, par construction même, le triangle cévien PQR de M par rapport à ABC est autopolaire pour la conique (c'est la construction de la première illustration de cette page). |
Il en résulte alors que si on prend deux point M et N sur la conique, les deux triangles cévients PQR et P'Q'R' sont autopolaires et donc que les 6 points P, Q, R et P', Q', R' sont sur une même conique.
Mais par 5 points quelconques A, B, C, M et N, il passe toujours une conique (M et N n'étant pas sur les côtés du triangle ABC elle n'est pas dégénérée). On retrouve alors un résultat déjà montré dans abraCAdaBRI à cette page en utilisant le théorème de Carnot (extraits) :
 |
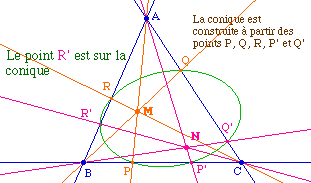Théorème : Les droites joignant les sommets d'un triangle à deux points donnés coupent les côtés opposés en six points qui sont sur une même conique. En effet, par Céva on a  Et donc par le théorème de Carnot, les 6 points sont sur une conique. |
Menu général