Triangles autopolaires,
applications à l'hyperbole
équilatère
3. Coniques harmoniquement
inscrites et circonscrites
[L'article de Géry
Huvent] [Retour
"Coniques"] [Menu
Général]
1. Triangles autopolaires et
théorème de Poncelet | 2.
Applications à l'hyperbole
équilatère
Dans cette page, les coniques sont supposées être non
dégénérées.
Remarque : les
figures de cette page sont réunies sur deux pages pour
être manipulées dans le navigateur, avec
CabriJava.
|
|
Rappel du vocabulaire usuel
On dita d'une conique qu'elle est
inscrite
à un triangle si elle est
tangente
à ces côtés, et qu'elle est
circonscrite
à un triangle si elle
passe
par ses sommets.
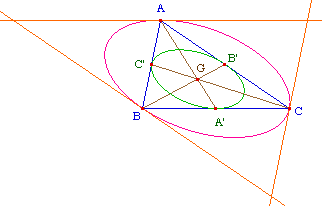
Ci-contre l'ellipse verte est
l'ellipse de Steiner
inscrite
à ABC, la rose est l'ellipse de Steiner
circonscrite
|
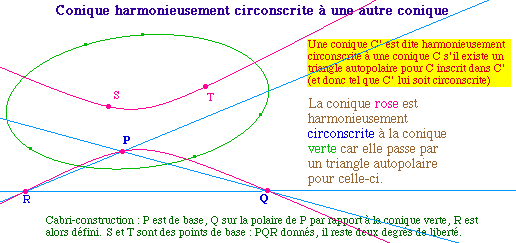
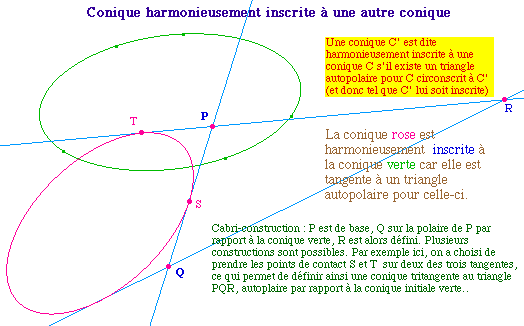
Définitions
 CnkHa01.fig - Voir la figure en
CabriJava
CnkHa01.fig - Voir la figure en
CabriJava
 CnkHa02.fig - Voir la figure en
CabriJava
CnkHa02.fig - Voir la figure en
CabriJava
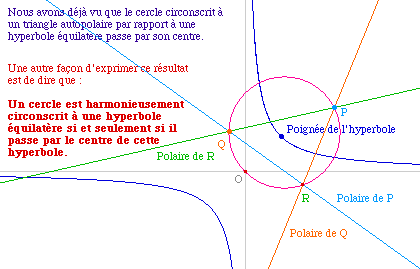
Un exemple
élémentaire : interprétation d'un
résultat précédent
 CnkHa03.fig
CnkHa03.fig
Caractérisations
algébriques
Par choix d'un repère projectif, les deux coniques C et C'
sont représentées par des matrices symétriques
inversibles A et B. Un changement de repère transforme ces
matrices en des matrices congruentes, toutefois, les deux
réels tr(BA-1) et tr(B-1A) sont
invariants. Géry Huvent montre dans son article que ces deux
invariants caractérisent les coniques harmonieusement
inscrites ou circonscrites. Il montre ainsi que :
Première caractérisation
:
Soient deux deux coniques C et C'
représentées par les matrices A et B dans un
repère. Alors C' est harmonieusement circonscrite à C
ssi tr(BA-1) = 0.
Au passage, sa preuve permet de voir que s'il y a un triangle
autopolaire, il y en a une infinité :

La Cabri-exploration
est une remarque du webmestre d'abraCAdaBRI. Elle n'engage pas
l'auteur de l'article ... au cas où ce serait faux ;-)
 CnkHa04.fig
CnkHa04.fig
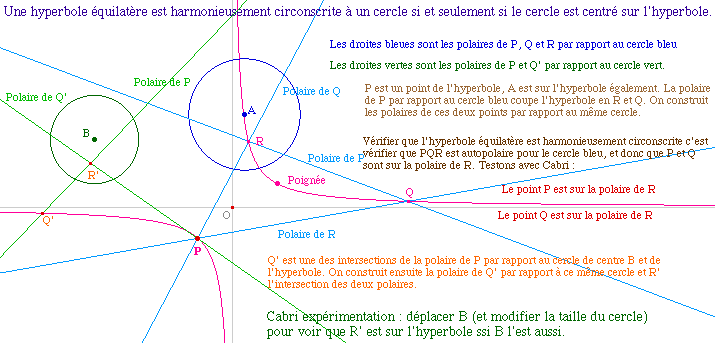
Cas de l'hyperbole
équilatère et du cercle : en appliquant
ce résultat algébrique au cas particulier du cercle
et de l'hyperbole équilatère, on aboutit à la
caractérisation suivante :
 CnkHa05.fig - Voir la figure en
CabriJava
CnkHa05.fig - Voir la figure en
CabriJava
Résultat qui pourrait se montrer
géométriquement, fait remarquer l'auteur, en
considérant le triangle de sommets le centre du cercle, et
les deux points à l'infini de l'hyperbole. Ce triangle est
autopolaire pour le cercle car les asymptotes sont orthogonales,
et il est inscrit dans l'hyperbole ssi le centre du cercle est sur
l'hyperbole.
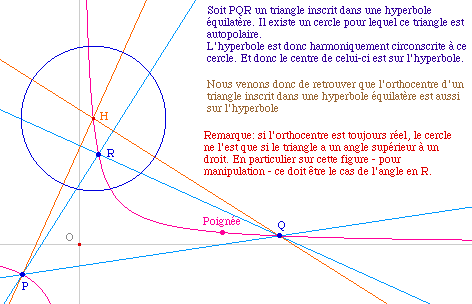
Où l'on retrouve l'orthocentre
d'un triangle inscrit ...
 TRAutoC3.fig
TRAutoC3.fig
Hyperbole passant par 4 points
orthocentriques
Soit PQR un triangle d'orthocentre H (différent des
sommets). Construisons une hyperbole passant par P, Q, R et H.
Soit C le cercle pour lequel PQR est autopolaire; il est
réel ou imaginaire, mais son centre est H. Il existe alors
un autre triangle autopolaire pour C : la polaire de H est la
droite de l'infini, elle coupe l'hyperbole en deux points X et Y,
les points à l'infini de l'hyperbole. D'une part ce
triangle est autopolaire pour C mais de plus, puisque H est le
centre de C, il est rectangle en C. Or les droite (HX) et (HY)
sont les directions asymptotiques de l'hyperbole et donc
l'hyperbole est équilatère. Nous retrouvons ainsi ce
résultat bien classique :
Une hyperbole passant par 4
points orthocentrique est équilatère.
Remarque : par ailleurs pour des questions de convexité,
cela ne peut être ni une ellipse, ni une parabole ... donc
une conique passant par 4 points orthocentrique est une hyperbole
équilatère.
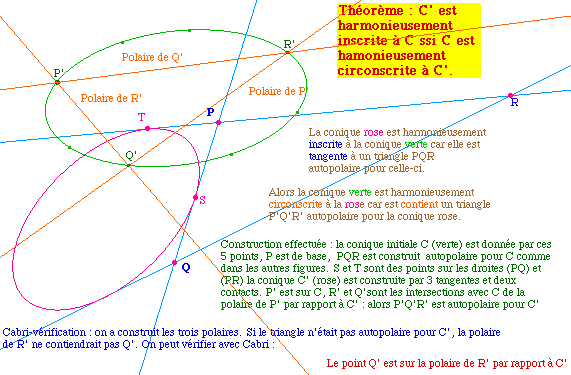
Seconde caractérisation
:
Soient deux deux coniques C et C'
représentées par les matrices A et B dans un
repère. Alors C' est harmonieusement inscrite à C ssi
tr(B-1A) = 0.
Les conséquences de cette seconde caractérisation -
montrée matriciellement par Géry Huvent - ne seront pas
développées pour elle-même, du fait qu'elle
amène une équivalence entre les deux notions :
 CnkHa06.fig - Voir la figure en
CabriJava
CnkHa06.fig - Voir la figure en
CabriJava
Nous allons terminer en développant cette
équivalence dans le cas des cercles et des hyperboles
équilatères.
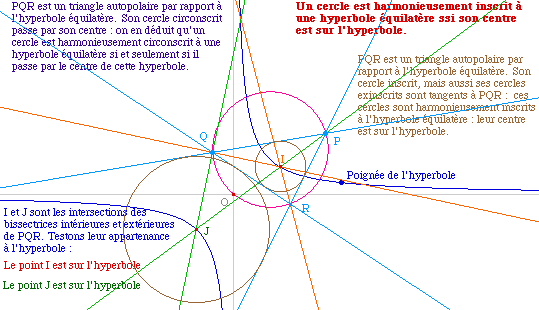
Applications
On a vu qu'une hyperbole équilatère est
harmoniquement circonscrite à un cercle si et seulement si
elle passe par le centre du cercle. On en déduit - de par les
caractérisations précédentes - qu'un cercle est
harmoniquement inscrit dans une hyperbole équilatère si
et seulement si son centre est sur cette hyperbole.
 CnkHa07.fig - Voir la figure en
CabriJava
CnkHa07.fig - Voir la figure en
CabriJava
C'est en particulier le cas pour tout triangle PQR cévien
d'un triangle inscrit ABC de l'hyperbole équilatère
(dont le centre cévien est aussi sur l'hyperbole) puisque l'on
sait qu'il est autopolaire pour l'hyperbole :

 CnkHa08.fig - Voir la figure en
CabriJava
CnkHa08.fig - Voir la figure en
CabriJava
Terminons par retrouver ainsi une propriété bien
connue du triangle orthique d'un triangle :
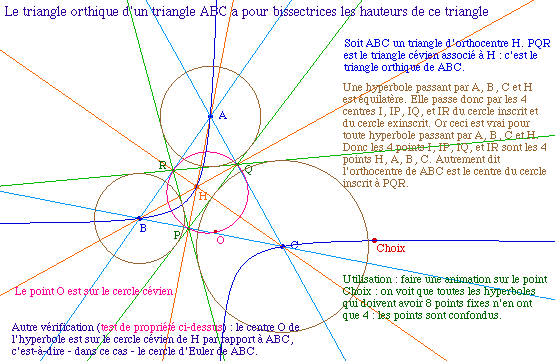
 CnkHa09.fig - Voir la figure en
CabriJava
(avec l'animation)
CnkHa09.fig - Voir la figure en
CabriJava
(avec l'animation)
Il faut bien s'arreter, et pourtant il y aurait encore tant et
tant à dire ...
1. Triangles autopolaires et
théorème de Poncelet | 2.
Applications à l'hyperbole équilatère
[L'article
de Géry Huvent] [Retour
"Coniques"]
 Menu général
Menu général
