Aspect affine (et projectif) des coniques Théorème de Carnot

 [Liste des constructions affines] [Coniques dans abraJava]

 Théorème de Carnot - Page 2

Présentation

Le théorème de Carnot, dans le cas du second degré - donc des coniques - a déjà fait l'objet d'un dossier d'une dizaine de pages dans abraCAdaBRI. Nous y renvoyons le lecteur pour les différentes preuves du théorème ou de ses applications. Dans cette pages, nous illustrons ses différents cas particuliers "génériques" usuels de manière dynamique et manipulable directement en ligne. Dans les autres pages, chaque cas particulier est détaillé avec précision.

Le théorème de Carnot

 

Théorème de Carnot Soient P et P' de (BC), Q et Q' de (CA), R et R' de (AB), différents des sommets. Alors les six points P, P', Q, Q', R et R' sont sur une même conique ssi : Preuve par les barycentres (dans abraCAdaBRI) Preuve par homologie harmonique (idem avec illustration de plusieurs cas particuliers dégénérés)

L'illustration est faite dans le cas particulier où chaque parenthèse ci-dessus est déjà égale à 1 : on ne peut déplacer que P, Q et R.

 

Cas particulier de deux triplets de céviennes concourantes

Théorème : Les droites joignant les sommets d'un triangle à deux points donnés coupent les côtés opposés en six points qui sont sur une même conique. En effet, par Céva on a Et donc par le théorème de Carnot, les 6 points sont sur une conique. La conique des neufs points (en CabriJava) Cas des céviennes parallèles (en CabriJava)

Les céviennes sont manipulables par les points M et N.

Cas particulier des points doubles

Si, dans la relation du théorème de Carnot, on identifie les points P et P', Q et Q', et R et R', la conique est tritangente au triangle. Par ailleurs la relation devient 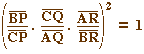 Si on exclu le cas où les trois points sont alignés (produit égal à 1 par Ménélaüs), alors le produit des trois termes est égal à -1, et, par le théorème de Céva, les droites (AP), (BQ) et (CP) sont parallèles ou concourantes. Illustration du passage à la tangente (CabriJava) Cas des céviennes parallèles (CabriJava) La construction de la conique (dans abraCAdaBRI)

Les céviennes sont manipulables par le point L. Penser à le sortir du triangle.

Autre cas particulier : les points symétriques par rapport aux milieux des côtés.

Si, sur la droite (BC), on a , cela signifie que et donc - avec équivalence - que P dans le repère (B, C) a même barycentre que P' dans le repère (C, B), ou encore que P et P' sont symétriques par rapport au milieu A' de [BC]. Il résulte ainsi du théorème de Carnot la propriété suivante :

Théorème : Soit ABC un triangle. On considère trois points P de (BC), Q de (CA), et R de (AB) autres que les sommets du triangle, et P', Q', R' les symétriques de P, Q et R par rapport aux milieux respectifs des côtés du triangle. Alors les six points sont sur une même conique.

C'est ce cas particulier qui est illustré dans la figure d'introduction.En voici un autre exemple avec le cercle inscrit et les cercles exinscrits :

Les contacts sur un même côté d'un triangle du cercle inscrit (orange ci-dessous) et du cercle exinscrit correspondant sont symétriques par rapport au milieu du triangle.
Ceci assure l'existence d'une première conique (verte ci-dessous) passant par ces 6 points.
Les contacts sur le même côté du triangle des deux autres cercles exinscrits sont eux aussi symétriques par rapport au milieu du côté.
Ceci assure l'existence de la seconde conique (en rose ci-dessous) passant par ces 6 points. Preuve détaillée de ces résultats (dans abraCAdaBRI)

 Théorème de Carnot - Page 2