Aspect affine (et projectif) des coniques Théorème de Carnot (2/2)

[Liste des constructions affines] [Coniques dans abraJava]

Théorème de Carnot - Page 1

Droites isotomiques

Soient (AB), (BQ), (CR) trois céviennes concourantes en M, et P', Q', R' les symétriques de P, Q, R par rapport aux milieux des côtés.

D'après le théorème de Carnot, dans le cas particulier des points symétriques, les 6 points sont sur une coniques. Puisque, par hypothèse on a :

. Il en résulte :

Et donc les droites (AP'), (BQ') et (CR') sont concourantes ou parallèles. On dit que ces trois céviennes sont les céviennes isotomiques des premières et - quand elles sont concourantes - que M' est l'isotomique de M pour ABC.

Ce résultat se montre bien entendu classiquement avec les barycentres. Il s'agissait ici de retrouver ce résultat sans calcul barycentrique, juste par une conique intermédiaire, grâce au théorème de Carnot.

Cas où les céviennes de départ sont parallèles : Dans le cas où les céviennes de départ sont parallèles, nécessairement les céviennes isotomiques sont concourantes. En effet, dans la situation de concourance, si

avec nécessairement

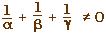
sinon les droites (AP'), (BQ') et (CR') sont parallèles comme illustré ci-dessouse, en réciproque à ce résultat.

Applications sur le cercle (retrouver Gergonne et Nagel) - dans abraCAdaBRI

Ellipse de Steiner et parabole tritangente à un triangle

On connait des arguments euclidiens sur les paraboles tritangentes à un triangle : le foyer doit être un point du cercle circonscrit au triangle (autre que les sommets) et la directrice est alors la droite de Steiner associée au foyer. On s'intéresse ici à l'aspect affine de la situation dans le cas d'une conique tritangente en les point d'intrsection de trois céviennes concourantes comme vu à la page précédente.

Dans la première illustration, P étant donné, on construit Q et R pour que la conique issue des céviennes concourantes (AP), (BQ) et (CR) soit une parabole. On observe alors le lieu du point de concours L quand P décrit (BC).

Remarque : le lieu n'est pas complet car Java ne calcule pas en dehors de la fenêtre.

On s'aperçoit alors que le lieu de L n'est rien d'autre que l'ellipse de Steiner circonscrite à ABC, ce qu'illustre la figure suivante :

Preuves de ce résultat (dans abraCAdaBRI)

Théorème de Carnot - Page 1