Modèle hyperbolique de Klein
- Beltrami
KB.1.b. Les macros de
géométrie projective
utilisées
[Introduction] [Orthogonalité
et symétries] [Cercles et
horocycles] [Angles]
[Coniques]
[Retour aux GNE]
[Le modèle de
Poincaré] [Historique
des GNE]
Toutes les macros
proposées dans cette page sont déjà
présentes dans la barre de menu du modèle de
Klein-Beltrami.
Division harmonique
|
|
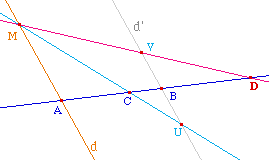
A, B étant donnés et C sur (AB). A partir
de tout point M d'une droite d passant par A, autre que
(AB), on construit l'intersection U de (MC) et de d',
parallèle à d passant par B. Soit alors V le
symétrique de U par rapport à B. La droite
(MV) coupe (AB) en un point D indépendant du point M
et de la droite d.
D est le conjugué harmonique de C par rapport
à (A,B). Et on a
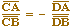
 DivHB1.fig
DivHB1.fig
|
Pour d'évidentes raisons de symétries dans
l'écriture du birapport, on dit que les couples (A, B) et (C,
D) sont en division harmonique.
Si on transforme cette figure en macro, on pourra observer qu'elle
a un bon comportement à l'infini : si C est le milieu de
[AB], on peut facilement vérifier que D existe
à l'infini dans la direction de (AB), ou encore si on fait
aller C à l'infini, on vérifie que D est bien milieu de
[AB]. Toutefois, cette constructon ne sera pas suffisante
dans nos utilisations pratiques : si on veut que la symétrie
orthogonale du modèle KB fonctionne dans tous les cas, nous
avons besoin que la macro division harmonique ait un comportement
valide aussi si A est à l'infini. Or, dans la figure
ci-dessus, le point sur objet de d qui devient la droite à
l'infini disparaît. Si on essaie d'améliorer cette
construction en prenant des points à distance finie,
préconstruits, toujours existants, cela ne fonctionne pas non
plus.
Pour réaliser une figure dans laquelle trois des 4 points
considérés peuvent aller à l'infini, il faut s'y
prendre autrement. On utilise pour cela une propriété
des quadrilatères complets relative à la division
harmonique (voir lien ci-dessous). Avec la construction suivante, on
a une solution plus générale pour la division
harmonique, satisfaisante aux exigences de passage à l'infini
dans la géométrie hyperbolique du modèle de
Klein Beltrami.
|
|
Détail de la construction
(un autre enchaînement peut faire perdre le bon
fonctionnement quand A est à l'infini).
A et B sont donnés, C est un
point de (AB).
On construit deux droite dA et dB
passant par A et B respectivement. Elles se coupent en
P.
Sur dB, on prend un point sur objet M.
La droite (CM) coupe dA en N. Les droites (AM) et (BN) se
coupent en Q.
(PQ) coupe (AB) en D cherché.
 DivHGene.fig ou DivHGene.mac
DivHGene.fig ou DivHGene.mac
On donne A, B, C dans cet ordre. B doit rester fini, A ou
C peuvent aller à l'infini.
|
Plus
de propriétés sur la division harmonique, pôles
et polaires (dont celle utilisée pour la macro ci-dessus)
Pôle d'une droite par rapport
à un cercle
|
|
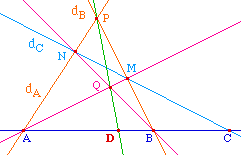
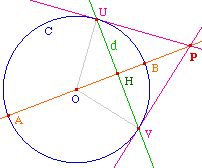
Etant donnés un cercle C et une droite d, on trace
l'intersection H de d et de sa perpendiculaire passant par
le centre du cercle. Cette dernière coupe le cercle
en A et B. On appelle Pôle de d par rapport à C
le conjugué harmonique P de H par rapport à
(A, B).
 PoleDrCr.fig (la figure
ci-contre) et PoleDrCr.mac
la macro associée, avec laqelle on peut tester de
diverses façons le comportement à l'infini,
quand la droite d passe par le centre O du cercle.
PoleDrCr.fig (la figure
ci-contre) et PoleDrCr.mac
la macro associée, avec laqelle on peut tester de
diverses façons le comportement à l'infini,
quand la droite d passe par le centre O du cercle.
Remarque :
dans la page liée ci-dessus, on trouvera la notion de
pôle et polaire dans un cadre plus
général : par rapport à des droites
sécantes, qui sont des coniques
dégénérées, et ensuite par
rapport à une conique et enfin par rapport à
un cercle, comme conique (affine ou projective)
particulière.
|
|
|
Une propriété du
pôle
On se servira essentiellement dans le modèle de
Klein-Beltrami du cas où la droite coupe le cercle en
deux points U et V. Alors dans ce cas le pôle de la
droite n'est autre que l'intersection des tangentes au
cercle en U et V, ce que l'on peut montrer par les relations
métriques dans le triangle rectangle.
On retrouve
que si H est en O, P est à l'infini dans la direction
de (AB).
|
Polaire d'un point par rapport à un
cercle
|
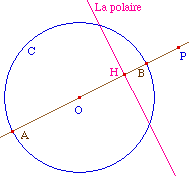
|
C'est la définition réciproque : à
partir de P on onstruit la droite (OP) et H conjugué
harmonique de P par rapport à A et B. La polaire est
la perpendiculaire à (OP) en H.
 PolaireC.fig et PolaireC.mac
PolaireC.fig et PolaireC.mac
La polaire
existe quand P est à l'infini - c'est un
diamètre - quand P est sur le cercle (ce sera un
point idéal du modèle de Klein-Beltrami) et
alors c'est la tangente au cercle en ce point. Elle n'existe
pas quand P est en O.
Il semble
que les trois cas n'étaient pas réalisables
simultanément. Ce dernier cas semble marginal dans le
cadre de la géométrie hyperbolique, la polaire
étant la droite de l'infini.
|
Homologie harmonique
|
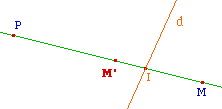
|
Etant donnés une droite d un point P,
l'application qui à un point M du plan associe le
point M' conjugué harmonique de M par rapport
à P et I où I est l'intersection de (PM) et de
d s'appelle l'homologie harmonique
d'axe d et de pôle P.
 HomoH1pt.fig et HomoH1pt.mac
HomoH1pt.fig et HomoH1pt.mac
L'homologue
harmonique, dans cette macro, existe si M est milieu de
[PI] ou si M est à l'inifini, mais
également si P est à l'infini. Dans le cas
où (PM) // d, M' existe encore, et c'est le
symétrique de M par rapport à P.
|
Quelques propriétés
de l'homologie harmonique :
Elle est involutive et conserve le contact. Les points
de l'axe (d) sont invariants et les droites passant par le
centre O sont globalement invariantes.
Elle conserve le birapport de 4 points alignés (donc la
conjugaison harmonique) et la polarité.
Soit A un point. Une conique est
globalement invariante par l'homologie de centre A et d'axe la
polaire de A par rapport à cette conique.
C'est cette
dernière propriété qui fait des homologies
harmoniques d'axe une droite coupant le cercle et de centre le
pôle de son axe les symétries orthogonales du
modèle de Klein Beltrami.
Elle
permet de transformer un cercle en une conique des trois types
affines.
Axe de l'homologie harmonique
|
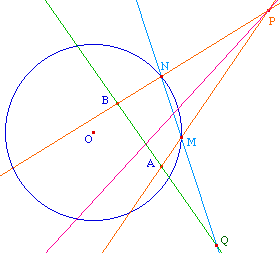
|
Cette construction est la seule de cette page qui soit
déjà orientée vers le modèle de
Klein-Beltrami dans la mesure où il y a une
infinité d'homologies harmoniques échangeant A
en B, y compris d'axes passant par P ci-contre,
mais une seule laisse le cercle
horizon invariant : c'est celle que l'on veut
construire.
A et B étant donnés, on construit le
pôle P de la droite (AB), puis M et N intersection du
cercle avec (PA) et (PB), et Q intersection de (MN) et (AB).
Alors l'axe cherché les la polaire de Q par rapport
au cercle.
 AxeHKB.fig et AxeHKB.mac
(objets initiaux les deux points A et B et le cercle)
AxeHKB.fig et AxeHKB.mac
(objets initiaux les deux points A et B et le cercle)
L'axe existe
si l'un des deux points est le centre du cercle (important
pour les mesures d'angles ou la présentation du
cercle hyperbolique). Il existe aussi quand A, O, B sont
alignés (un pôle est à l'infini) y
compris quand O est milieu de [AB]. L'axe existe
aussi quand A et B sont idéaux pour le modèle
hyperbolique, c'est-à-dire sur le cercle.
|
La construction précédente est basée
sur les propriétés des homologies harmoniques
déjà
mentionnées.
La figure ci-dessous illustre qu'une
seule homologie harmonique échangeant A en B - et
d'axe passant par le pôle de (AB) par rapport au cercle,
laisse ce cercle invariant et donc peut
prétendre à être une isométrie du
modèle de Klein-Beltrami.

 AxeHFaux.fig
AxeHFaux.fig
Bien-sûr cet
axe est la médiatrice hyperbolique de [AB] pour le
modèle de Klein-Beltrami, d'où la précaution de
construction ...
[Introduction] [Orthogonalité
et symétries] [Cercles et
horocycles] [Angles]
[Coniques]
[Retour aux GNE]
[Le modèle de
Poincaré] [Historique
des GNE]
 Menu général
Menu général







