[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Bissectrices] [Coniques]
[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]

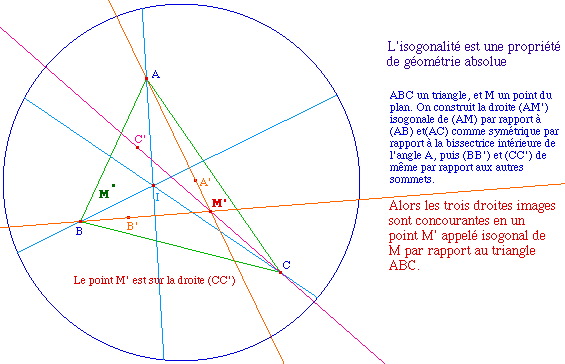
Toutefois, beaucoup de résultats sur l'isogonalité en géométrie euclidienne ne se retrouvent pas en géométrie hyperbolique. Par exemple des couples "célébres" de points isogonaux ne le sont plus hyperboliquement, comme le centre du cercle circonscrit O et l'orthocentre H, ou encore les points de Gergonne et de Nagel.
De même certaines propriétés des couples isogonaux n'existent plus. On pourra par exemple vérifier que les projections de M et M' sur les côtés du triangle ne sont plus six points cocycliques comme en géométrie euclidienne. Il serait intéressant d'approfondir les propriétés absolues de l'isogonalité.
Rappelons qu'en géométrie euclidienne deux points isogonaux sont foyers d'une conique tritangente aux côtés d'un triangle ... d'où un intérêt certain pour cette notion ;-)
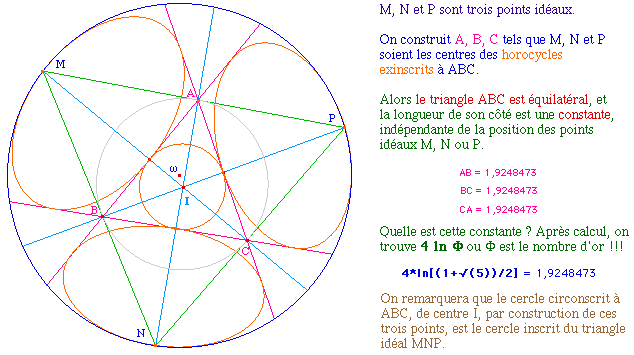
On s'intérese à la construction d'un triangle ayant trois horocycles exinscrits. Alors ce triangle a une propriété remarquable, déjà mentionnée dans abraJava à cette page pour le modèle du disque de Poincaré. Illustrons là dans le modèle de Klein-Beltrami.
4.a. Bissectrices intérieures | 4.b. Bissectrices extérieures | 4.d. La construction de Malfati
[Introduction] [Orthogonalité et symétries] [Cercles et horocycles] [Bissectrices] [Coniques]
[Retour aux GNE] [Le modèle de Poincaré] [Historique des GNE]