 |
|
[Plan de cette partie] [Conséquences des axiomes] [Les Faisceaux]
Preuves ou illustrations en CabriJava du : Th 10 | Th 11 | Th Hjelmslev | d = abc | Droite de F(ab)
 |
|
[Plan de cette partie] [Conséquences des axiomes] [Les Faisceaux]
Preuves ou illustrations en CabriJava du : Th 10 | Th 11 | Th Hjelmslev | d = abc | Droite de F(ab)
En fait il s'agit d'une lecture algébrique que propose Bachmann du théorème fondamental des plans métriques, comme nous le verrons plus loin.
Les axiomes 3 et 4 portaient sur la composée de trois droites dans le cas des faisceaux à centre ou à axe. Il s'agit ici d'observer le produit de points et de droites, plus précisément de caractériser quand AbC est une droite et quand aBc est un point.
Th 10 : AbC est une droite ssi il existe une droite v telle que v | A, b, C
On retiendra en pratique - sauf cas bien particuliers - que AbC est une droite ssi (AC) est orthogonale à b.
Complément : Dans le cas où AbC est une droite d, et v une droite telle que v | A, b, C alors d | v.
Th. 11 : aBc est un point ssi il existe une droite v telle que v | a, B, c
Là encore, on peut retenir d'une manière pratique que aBc est un point ssi B est sur la perpendiculaire commune à a et b.
Complément : Dans le cas où aBc est un point D, et v une droite telle que a, B, c | v, alors D | v.
Page de preuves des théorèmes et constructions sans CabriJava
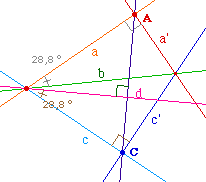 |
Ce théorème fondamental des plans métriques est une autre lecture du théorème 10. Soient, a, a', b, c, c' cinq
droites telles qu aa' = A, cc' = C, avec A et C distincts et
telles que abc soit une droite d. Dans l'illustration (ici en .gif) euclidienne de faisceaux à centre, on peut vérifier abc = d soit ab = dc par les angles. |
Voir des illustrations dynamiques CabriJava dans les différents modèles hyperboliques | dans le modèle elliptique
Outre un critère important (qu sera largement utilisé ultérieurement) pour que trois droites soient en faisceau, ce théorème donne une construction pratique de la quatrième droite d = abc produit de trois droites en faisceau. On en déduit la construction de la droite d'un faisceau donné passant par un point donné.
La quatrième réflexion
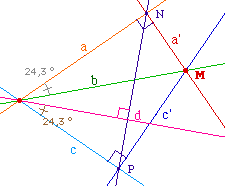 |
Principe de la construction dans Cabri Soit M un point sur objet de b, N et P sur a et c respectivement, telles que (MN) | a et (MP) | c. La droite d cherchée est la (une ?) perpendiculaire à (NP) appartenant au faisceau. Illustrée ci-contre dans le cas des faisceaux à centre dans le contexte euclidien, il convient de savoir construire la perpendiculaire à une droite donnée appartenant à un faisceau donné, ce qui ne pose aucxun porblème dans les modèles utilisés. |
Voir cela en détail en CabriJava : pour les modèles hyperboliques | Pour le cas elliptique
Droite du faisceau F(ab) passant par un point M
Deux droites a' et c' (distinctes) étant données. Pour tout point P non incident à l'une d'elle, il existe une droite incidente à ce point appartenant au faisceau F(a'c').
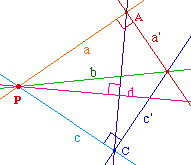 |
Principe de la construction dans Cabri a' et c' étant deux droites distinctes, on construit les deux perpendiculaires a et c aux droites a' et c' respectivement, passant par P. Notons alors A = aa' et C = cc'. Si A = C, alors A | c' et la droite A convient. |
Voir cela en détail en CabriJava : pour les modèles hyperboliques et elliptique
Preuves ou illustrations en CabriJava du : Th 10 | Th 11 | Th Hjelmslev | d = abc | Droite de F(ab)
[Plan de cette partie] [Conséquences des axiomes] [Les Faisceaux] [Géométrie absolue]
|
 Retour sur
"abra-Java"
Retour sur
"abra-Java" |