La figure GLTrace1.fig

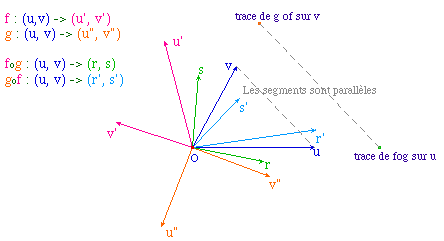
Si u' et v' ont pour coordonnées u'(a, b) et v'(c, d) dans la base (u, v), la trace de l'application linéaire est le nombre a + d. L'intérêt d'une construction géométrique est essentiellement pour l'utilisation de la notion de mesure algébrique pour construire ce nombre dans un repère donné.

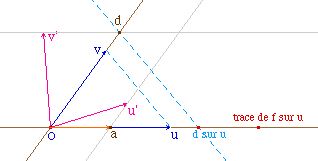
On construit simplement a et d par projection. On reporte ensuite d sur la direction du vecteur u. Le point obtenu ("d sur u") est ainsi d'abscisse, dans le repère (O, u) celle de d dans le repère (O, v). Par translation de vecteur Oa, de ce dernier point, on construit la somme dans le repère (O, u).

La macro TraceAL.mac : objets initiaux u, v, u', v', objet final le point "trace de f sur u".

Une illustration de cette indépendance peut être faite par exemple de la façon ci-contre, dans laquelle, on jongle entre l'espace vectoriel et l'espace affine sous-jacent :

La figure GLTrace2.fig

La même démarche peut être utilisée pour illustrer le théorème du titre. Dans la figure suivante, on a construit la trace de fog sur u et celle de gof sur v. Pour cela, on applique la macro Trace aux vecteurs (dans l'ordre) v, u, s' et r'. La trace est ainsi construite sur v. La vérification d'égalité se résume à vérifier que la droite passant par les deux points construits est parallèle à (uv) - identification, dans le plan affine, des vecteurs à leurs extrémités.

La figure GLTrace3.fig