Groupe linéaire
Macros de base sur GL2(R)

 

[Illustration : commutant] [Trace] [Déterminant] [Illustration : endomorphisme de trace nulle]

[Réduction des endomorphismes] [Adjoint d'un endomorphisme]

 

Pour construire l'image d'un vecteur par une application linéaire avec Cabri II, plusieurs approches sont possibles :

- considérer le plan vectoriel comme un espace affine pointé et utiliser le travail déjà effectué sur les applications affines.

- opérer de manière purement analytique, en construisant géométriquement les objets nécessaires.

- utiliser toutes les potentialités de Cabri II pour simplifier l'approche analytique précédente.

 

Nous allons illustrer la première et la troisième approche. La seconde, trop lourde ici, mériterait néanmoins d'être explicitée une fois : nous le ferons dans les items suivants sur des situations moins lourdes.
 

 

Première construction : vectorialisation d'un espace affine

La réalisation suivante utilise les transformations affines
Charger la macro TAff1pt.mac qui construit l'image d'un point M par une transformation affine dont on connait 3 points et leurs images.

Les vecteurs ont tous pour origine un point O (le plan affine naturel de Cabri est ainsi vectorialisé). La donnée d'une base (vecteurs OA et OB) et de son image (vecteurs OA' et OB') est équivalent à la donnée de l'application affine qui transforme le repère (O, A, B) en (O, A', B').
Comme dans une macro de Cabri on ne peut pas utiliser deux fois le même point en objet initial, pour appliquer la macro précédente au point M (ie au vecteur OM dans le vectorialisé), on a construit ci-contre le point O' symétrique de O par rapport à la droite (OA), ce qui permet d'appliquer la macro à O, A, B, O', A', B' et M.

Remarque : Tout comme la macro TAff1pt.mac, cette construction de l'image d'un vecteur par une application linéaire est aussi opérationnelle dans le cas où l'image (O, A', B') n'est pas un repère affine, c'est-à-dire dans le cas où l'application vectorielle n'est pas inversible.

Lancer la figure GLMac01.fig ci-dessus.

La transformation en macro permet de concrétiser le passage à la géométrie vectorielle en donnant comme objets initiaux les vecteurs de base (u, v) et leurs images (u', v') ainsi que le vecteur w dont on veut l'image.

Charger la macro ImAL1.mac associée.

Notons que l'on peut déjà illustrer l'existence de direction propre, en choisissant correctement les vecteurs images ...

On peut par exemple faire varier les vecteurs u' ou v' pour qu'une direction w donnée devienne direction propre.

Un premier objectif de ces pages va être la construction des directions propres.

Choix d'une autre méthode

En examinant les fichiers, on observe que la construction précédente aboutit à une macro qui réalise l'image d'un vecteur en 32 objets intermédiaires. Comme cette macro va être régulièrement utilisée pour tout ce qui touche à la géométrie vectorielle, il est naturel d'essayer d'optimiser cette macro. Nous allons diviser le nombre d'objets intermédiaires par deux, en utilisant les outils spécifiques à Cabri II (sur l'invitation appuyée de Eric Hakenholz ici remercié). Ce qui précéde illustrant alors simplement que cette construction est réalisable avec les prémisses élémentaires de la géométrie.

 

Seconde construction : approche analytique

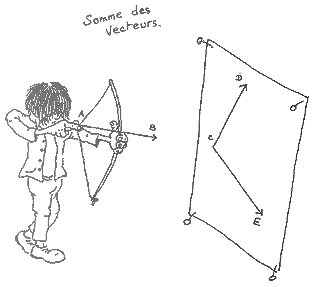
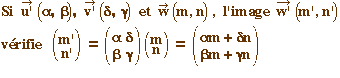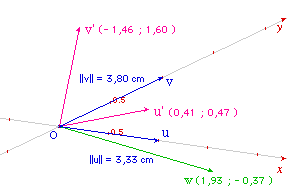
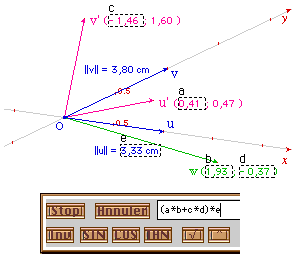
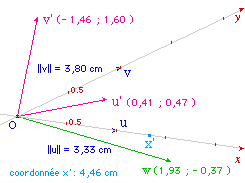
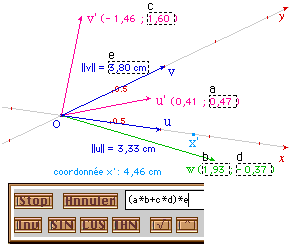
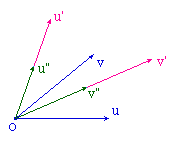
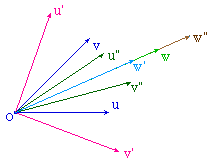
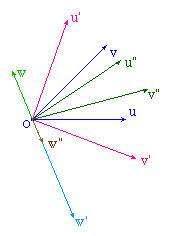
L'idée est tout simplement d'utiliser les calculs ordinaires d'algèbre linéaire, dans le repère définie par la base de vecteurs (u, v).

Cabri permet d'utiliser ce repère. Toutefois, si les coordonnées sont bien exprimées dans le repère, l'outil de report d'une longueur fonctionne avec des cm (signés). C'est la raison pour laquelle il faudra multiplier la composante x par la norme de u et celle en y par la norme de v avant de faire le report sur l'axe.

Remarque : Cette drnière multiplication (*e ci-dessous) n'est nécessaire que dansla version 1.1.5 que Cabri (DOS + Mac) mais pas dans la version 1.1.8 (Windows + Mac). Les illustrayions sont dans la version 1.1.5.

TOUTES LES FIGURES FINALES SONT PROPOSEES EN 1.1.5 et 1.1.8

Lancer la figure GLMac02.fig ci-dessus en l'état pour effectuer les opérations décrite ci-aprés :

 

coordonnée x'

 

Il suffit, dans la calculatrice de Cabri, d'appliquer l'écriture matricielle ci-dessus (c'est le terme ab+cd) que l'on multiplie par la norme de u.

Remarque : On ne s'inquiètera pas de la présentation de la calculatrice de Cabri sur cette illustration : abraCAdaBRI est réalisé sous environnement Mac OS, qui offre une grande panoplie de personnalisations.

Puis on reporte le résultat obtenu (par l'outil report de mesure) directement sur l'axe.

Dans Cabri, le report de mesure sur un axe est un report signé (ie algébrique) car le nombre est algébrique et l'axe orienté.

On a ainsi l'abscisse x' de w'.

 

Lancer la figure GLMac03.fig ci-dessus en l'état pour construire y'. (Cabri 1.1.5)

coordonnée y'

idem

Ayant reporté le dernier calcul sur l'axe des ordonnées, on construit alors le point w', image de w.

La figure GLMac04.fig terminée (Cabri 1.1.5)

La macro ImVectAL.mac associée.(Cabri 1.1.5)

Remarque : Sur une figure, on peut comparer les deux macros, la première issue de considérations barycentriques sur les transformations affines et la seconde provenant d'un calcul matriciel, pour vérifier qu'elles donnent bien le même vecteur. La seconde macro ne construit que 16 objets au lieu de 32 pour la première.

Enfin, il peut être utile de ne pas répéter deux fois l'application de la macro précédente et avoir directement l'image d'une base par une application linéaire :

Charger la macro ImBaseAL.mac
(Cabri 1.1.5)

illustration : une valeur propre positive et l'autre négative

Application inverse

En utilisant la macro précédente à l'application linéaire qui envoie (u', v') sur (u, v) pour la base (u, v) - et donc avec Cabri, par exemple les symétriques de u et v par rapport aux axes sous-jacents - on peut facilement construire une macro d'inversion :

Charger la macro InverseAL.mac (Cabri 1.1.5)

Exemples d'illustration

En déplaçant u' et v', on peut trés facilement obtenir la situation ci contre :

Reconnaît-on un type d'application linéaire connu ?

Ici, w' = f(w) et w" = f-1(w). On illustre ainsi que, quand elles existent, les directions propres de f-1 sont aussi celles de f.

Remarque : Si cette dernière propriété est triviale, son illustration - au cours d'une séance de formation par exemple - permet de vérifier que les constructions sont correctes. Cette activité peut donc être présenté comme une phase de validation personnelle des réalisations précédentes.

 

 [Illustration : commutant] [Trace] [Déterminant] [Illustration : endomorphisme de trace nulle]

[Réduction des endomorphismes] [Adjoint d'un endomorphisme]

 

Menu général