Plan vectoriel euclidien
Adjoint d'un endomorphisme

[Directions propres de l'adjoint] [Adjoint et symétrie (vers auto-adjoint]
[Construction d'endomorphismes auto-adjoints] [Directions propres des auto-adjoints] [Cas particulier de f* o f]

 [Groupe linéaire GL2(R)] [Réduction des endomorphismes]

 

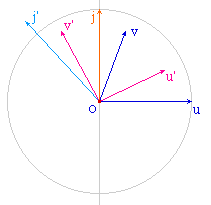
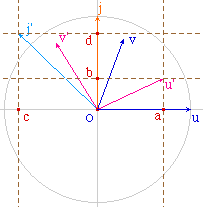
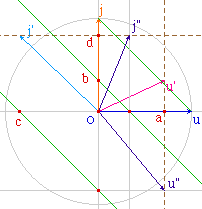
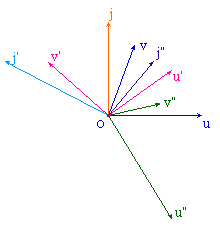
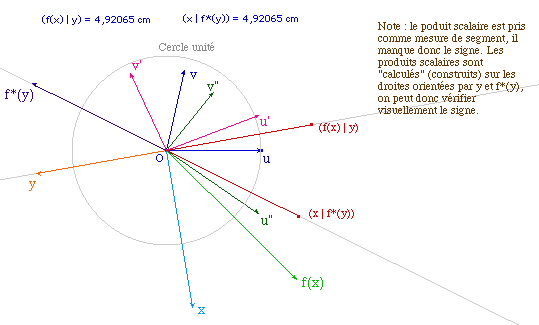
Dans un espace vectoriel muni d'un produit scalaire (.|.), on appelle adjoint d'un endomorphisme f, l'application f* telle que (f(x) | y) = (x | f*(y)). On sait que l'adjoint existe et est un endomorphisme.

Cette page se propose de construire l'application adjointe f* d'un endomorphisme f. Les pages suivantes illustreront quelques propriétés classiques de l'adjoint.

 

La construction de l'adjoint d'un endomorphisme f et des directions propres de f*of sont les thèmes à l'origine de la partie vectorielle d'abraCADaBRI.
 

Les figures de description sont en 1.1.5, les figures ou macros finales sont proposées aussi en 1.1.8.

Principe de la construction

On sait que dans une base orthonormée, la matrice M* de f* est la transposée de la matrice M de f. Etant donnée une base quelconque (u,v), et (u', v') son image par f, on peut construire l'image d'une base orthonormée (i, j), et dans cette base construire f*(i) et f*(j). Ayant une base et son image, on peut construire l'image par f* de u et v.

Concrètement, on peut choisir comme premier vecteur i de la base orthonormée le vecteur u. En effet, l'important pour avoir M* = tM est d'avoir une base orthogonale formée de deux vecteurs de même norme. En termes d'objets à construire, cette remarque simplifie la construction de moitié.

Pour faire la figure en ligne, il est utile de

Charger la macro ImVectAL.mac (1.1.5) ou ImAL1.mac (les deux versions) qui construit l'image d'un vecteur par une application linéaire.

 

Construction de l'adjoint d'un endomorphisme

a - Image d'une base orthogonale de vecteurs de même norme

Comme indiqué dans la présentation, on construit j orthogonal à u et de même norme, et la macro ci-dessus permet de construire son image j'.

Ainsi l'endomorphisme f est défini par l'image d'une base "orthonormée". On va pouvoir construire l'adjoint par transposition.

La figure de départ Adjoint1.fig (1.1.5) ci contre.

b - Image de la base orthonormée par l'adjoint

Dire que M* = tM signifie que si, dans la base (u, j) on a u' de coordonnées (a, b) et j' de coordonnées (c, d), alors u" = f*(u) est de coordonnées (a, c) et j"=f*(j) est de coordonnées (b, d). La construction est alors élémentaire :

Adjoint2.fig (1.1.5) en l'état (u" et j" construits).

c - Image de la base de départ

On dispose dont d'une application f* dont on connait l'image (u", j") d'une base (u, j). La macro d'introduction permet de construire l'image v" de v.

On a donc construit l'adjoint f* de l'endomorphisme f.

La figure Adjoint3.fig (1.1.5) finale.

 

La macro Adjoint.mac (1.1.5) ou Adj118.mac (1.1.8) associée : pour distinguer u" de v", le vecteur u" est désigné sous le curseur par l'expression "Image du premier vecteur de la base".

Vérification par la définition

VerifAdf.fig (1.1.8 seulement)

 

Les pages suivantes proposent quelques illustrations simples des propriétés de l'adjoint d'un endomorphisme.

 

 [Directions propres de l'adjoint] [Adjoint et symétrie (vers auto-adjoint]
[Construction d'endomorphismes auto-adjoints] [Directions propres des auto-adjoints] [Cas particulier de f* o f]

  [Groupe linéaire GL2(R)] [Réduction des endomorphismes]

 

Menu général